Целевая переменная в модели частичного приспособления имеет вид

a)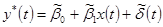

b)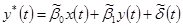

c)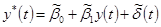

d)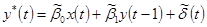

12. Если в методе последовательных разностей 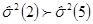, а 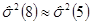, то неслучайная составляющая аппроксимируется полиномом степени

a)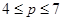

b)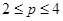

c)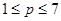

d)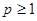

13. Если общий линейный процесс описывается классической линейной моделью множественной регрессии, то он имеет вид =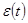

a)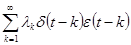

b)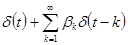

c)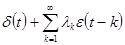

d)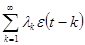

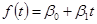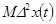14. Если неслучайная составляющая временного ряда х(t) имеет линейный вид , то равно

a) 0

b) 1

c)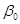

d)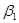

15. Сглаженное значение 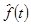вычисляется по формуле

a)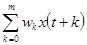

b)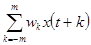

c)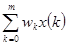

d)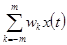

Для идентификации АР и СС моделей сначала делают оценки

a) автокорреляционной функции

b) частной автокорреляции

c) автоковариационной функции

d) спектральной плотности

В модели АР(1) частная автокорреляционная функция случайных остатков, разделенных двумя тактами времени, равна

a)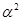

b)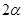

c) 1

d) 0