1. Пусть вектор 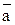 параллелен вектору
параллелен вектору  1, тогда существует x ÎR такое, что
1, тогда существует x ÎR такое, что 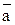 = x
= x  1.
1.
2. Пусть векторы лежат в плоскости П и  1 не параллелен
1 не параллелен  2. Тогда всякий вектор
2. Тогда всякий вектор 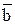 ÎП есть линейная комбинация векторов
ÎП есть линейная комбинация векторов  1 и
1 и  2:
2:
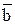 = х
= х  1 + у
1 + у  2.
2.
3. Пусть векторы  1,
1,  2 и
2 и  3 не лежат в одной плоскости. Тогда всякий вектор
3 не лежат в одной плоскости. Тогда всякий вектор 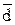 есть их линейная комбинация:
есть их линейная комбинация:
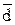 = x
= x  1 + y
1 + y  2 + z
2 + z  3
3
 Доказательство проведем только для случая 2.
Доказательство проведем только для случая 2.
Выберем произвольную точку О на плоскости П и отложим из нее векторы  1,
1,  2 и
2 и 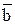 . На направления О
. На направления О  1 и О
1 и О  2 отложим направленные проекции вектора
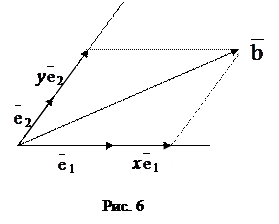
2 отложим направленные проекции вектора 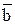 , рис. 6, обозначив их, соответственно, х
, рис. 6, обозначив их, соответственно, х  2 и у
2 и у  2. Тогда получим требуемое равенство
2. Тогда получим требуемое равенство 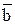 = х
= х  1 + у
1 + у  2. Случай 2 доказан. Случай 1 - тривиален, а случай 3 доказывается аналогично с построением параллелепипеда.
2. Случай 2 доказан. Случай 1 - тривиален, а случай 3 доказывается аналогично с построением параллелепипеда.
Будем говорить, что векторы  1 и
1 и  1, рис. 6, образуют векторный базис на плоскости векторов, а числа х и у назовем координатами вектора
1, рис. 6, образуют векторный базис на плоскости векторов, а числа х и у назовем координатами вектора 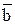 в этом базисе. Аналогично можно определить базис на прямой и в пространстве, используя случаи 1 и 3 рассмотренной теоремы.
в этом базисе. Аналогично можно определить базис на прямой и в пространстве, используя случаи 1 и 3 рассмотренной теоремы.
Таким образом, каждый вектор имеет свои координаты в заданном базисе и, наоборот, всякая тройка чисел (x,y,z) (в заданном порядке) определяет единственный вектор в этом базисе.
 2015-05-18
2015-05-18 354
354








