Если в пространстве задан базис {  1,
1,  2,
2,  3}, то между множеством векторов и упорядоченными тройками чисел (x,y,z) установлено взаимно-однозначное соответствие
3}, то между множеством векторов и упорядоченными тройками чисел (x,y,z) установлено взаимно-однозначное соответствие
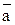 ↔(x,y,z), (1)
↔(x,y,z), (1)
определяемое разложением вектора 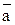 в заданном базисе:
в заданном базисе: 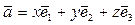 .
.
Чтобы объявить множество упорядоченных троек чисел 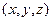 арифметической или координатной моделью трехмерного векторного пространства, покажем, что операции сложения векторов и умножения на число определена в координатной форме и, что координаты вектора определяют его длину и направление.
арифметической или координатной моделью трехмерного векторного пространства, покажем, что операции сложения векторов и умножения на число определена в координатной форме и, что координаты вектора определяют его длину и направление.
Для удобства будем считать, что 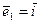 ,
, 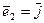 ,
, 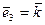 – известный в элементарной геометрии базис, состоящий из единичных взаимно-перпендикулярных векторов. Для простоты, также, ограничимся случаем плоскости.
– известный в элементарной геометрии базис, состоящий из единичных взаимно-перпендикулярных векторов. Для простоты, также, ограничимся случаем плоскости.
Пусть 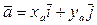 ,
, 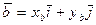 . Тогда
. Тогда 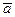 и
и 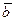 элементы геометрической модели и для них определена сумма
элементы геометрической модели и для них определена сумма
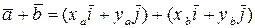 .
.
Учитываем, что 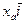 ,
, 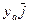 ,
, 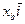 и
и 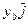 также элементы геометрической модели и, используя свойства 1-4 сложения и свойства 1-4 умножения, получаем:
также элементы геометрической модели и, используя свойства 1-4 сложения и свойства 1-4 умножения, получаем:

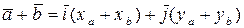
Согласно соответствию (1), установленному выше, заключаем, что 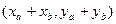 – координаты вектора
– координаты вектора 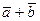 . Аналогично показывается, что вектор
. Аналогично показывается, что вектор 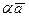 имеет координаты
имеет координаты 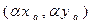 .
.
Используя теорему Пифагора, находим длину вектора на плоскости
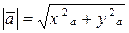
и в пространстве
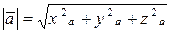 .
.
Наконец, для противоположного вектора 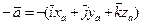 находим координаты:
находим координаты: 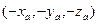 .
.
 2015-05-18
2015-05-18 320
320








