Использование трендовых моделей. Метод наименьших квадратов

Рассматривая зависимости между признаками, выделяют две категории связи: функциональные и корреляционные. Функциональные связи характеризуются полным соответствием между признаками. Функциональная зависимость может связывать результативный признак с одним или несколькими факторными признаками.

В корреляционных связях между изменением факторного и результативного признака нет полного соответствия, воздействие отдельных факторов проявляется лишь в среднем при массовом наблюдении фактических данных[2].

Метод наименьших квадратов является количественным и применяется, когда помимо данных измерений некоторой экономической величины Y в дискретные моменты времени имеются еще и теоретические данные о потенциальной форме кривой Y(t), т.е. известно, что зависимость параметра Y от времени t «вписывается» в формулу Y(t)=F(c₁, c₂,…, c_m, t), где величины (c₁, c₂,…, c_m) в нашем случае пока неизвестны. Метод наименьших квадратов, рассматриваемый ниже, представляет собой в некотором смысле «соединение теории с практикой»[3].

Итак, пусть некоторая экономическая величина Y измерена в дискретные моменты времени t₁, t₂, …, t_n: получены её значения y₁, y₂, …, y_n. Известно, что теоретическая зависимость Y(t) должна принадлежать некоторому классу функций F(c₁, c₂, …,c_m, t), т.е. зависимость y(t) известна нам с точностью до нескольких постоянных c₁, c₂, …, c_m. Данные измерений величины Y могут иметь ошибки, не носящие, однако, систематического характера. Требуется подобрать зависимость Y(t) из заданного класса функций с тем расчётом, чтобы ошибка такого подбора была минимальной, т.е. определить значения неизвестных c₁, c₂, …, c_m, лучше всего подходящие проведенным измерениям (t_i, y_i).

В качестве ошибки подбора функции метод наименьших квадратов рассматривает сумму квадратов отклонений значений y_i в каждой точке от значений подобранной функции F(c₁, c₂, …,c_m, t_i):

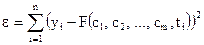. (1)

Для минимизации этой функции 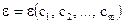(дело в том, что значения t_i и y_i для конкретной задачи являются постоянными и в расчёт не принимаются) используются условия (33):

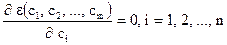. (2)

Формулы (2) в некоторых случаях (достаточно простой вид функции F(c₁, c₂, …,c_m, t), либо приводимый к линейному виду) позволяют определить недостающие значения c₁, c₂, …,c_m и решить, таким образом, поставленную задачу. При найденных значениях неизвестных c₁, c₂, …,c_m мы получаем явный вид зависимости Y(t), что позволяет проводить прогнозирование для произвольных значений t путём подстановки значений t в полученную функцию. Точность прогнозирования будет тем выше, чем меньше мы отклоняемся от точки проведения последних измерений (t_n, Y_n).

Рассмотрим задачу, связанную с линейной регрессией. Пусть имеются данные о ценах на некоторый вид ресурсов в некоторые дискретные моменты времени. Необходимо спрогнозировать значение цен в будущие моменты времени (экстраполяция) и определить, какими (ориентировочно) могли быть цены в моменты времени, когда наблюдения не производились (интерполяция). Зависимость цены от времени считать линейной.

Будем обозначать цену ресурса через P, а время – через t. Тогда функция ошибки e равна:

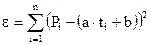. (3)

Вычислим её частные производные:

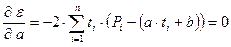, (4)

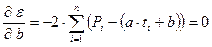. (5)

Преобразовав оба выражения, получим систему линейных алгебраических уравнений:

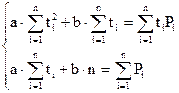(6)

Решим систему (37) методом Крамера, получим:

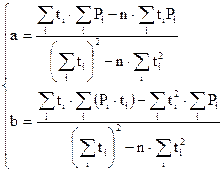(7)

Многие компьютерные программы уже содержат встроенные функции для построения линейных и нелинейных регрессий (например, в системе MathCAD – функции slope и intercept; для построения линейной комбинации произвольных функций – linfit), что избавляет пользователя от их ручного набора. В случае, когда зависимость Y(t) не является линейной, метод наименьших квадратов может не дать требуемого результата из-за сложности получаемых выражений (2) для поиска неизвестных констант c₁, c₂, …,c_m. По этой причине может применяться линеаризация, т.е. сведение нелинейной функции к линейному виду путем алгебраических преобразований.

Точность подбора функции может определяться с помощью коэффициента линейной корреляции r. Чем ближе число r по модулю к единице, тем вероятнее линейная зависимость между параметрами t и y (если 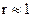, то зависимость, скорее всего линейная и растущая; при 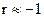зависимость между параметрами, скорее всего линейная и падающая). Коэффициент 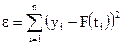даёт абсолютную оценку точности подбора любой функции к любым точкам. Он является мерой погрешности в методе наименьших квадратов (иногда, когда значения y являются достаточно большими, значения этого коэффициента могут быть велики, даже если точки расположены достаточно близко к аппроксимирующей кривой). Коэффициент 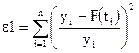даёт относительные погрешности, но его нельзя применять, если хотя бы одно из значений y равно нулю.