Следующим шагом является определение доверительных интервалов для зависимой переменной.
В данном случае используется два подхода для прогнозирования индивидуального значения зависимой переменной.
Первый подход – составляется статистика, вида:
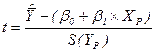 ,
,
Которое имеет распределение Стьюдента с числом степеней свободы n-2.
По таблицам критических распределений Стьюдента определяется критическое значение 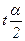 , n-2, удовлетворяющее условию:
, n-2, удовлетворяющее условию:
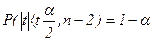 .
.
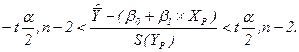
Если преобразовать представленный выше интервал к значениям a и b, то получим:
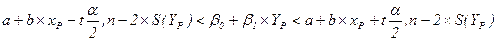
Доверительный интервал для среднего значения S(YP) зависимой переменной, покрывающий теоретическое значение с вероятностью 1-α определяется по формуле:
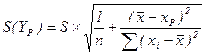 .
.
Второй подход – прогнозирование индивидуальных значений зависимой переменной. Построение формулы для данного подхода аналогично первому подходу, только:
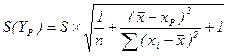
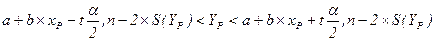
 2015-05-18
2015-05-18 260
260








