2015-05-18
2451
Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Аддитивную модель временного ряда формируют следующие значения компонент уровня временного ряда …
| yt = 7; T = 6,5; S = 0; E = -0,5 | |||
| yt = 7; T = 3,5; S = -2; E = -1 | |||
| yt = 7; T = 7,5; S = 0; E = -0,5 | |||
| yt = 7; T = 3,5; S = 2; E = 1 |
Изображенный на рисунке временной ряд содержит следующие компоненты:
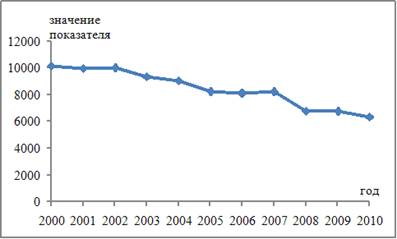
| убывающую тенденцию и случайную компоненту | |||
| возрастающую тенденцию и случайную компоненту | |||
| убывающую сезонную компоненту и случайную компоненту | |||
| сезонную компоненту и убывающую случайную компоненту |
Ряд, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, изображен на графике …
1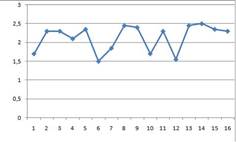 
| |
2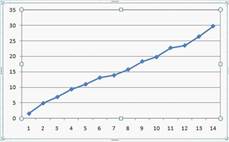 
| |
3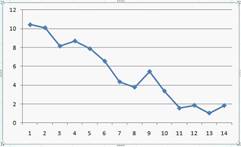 
| |
4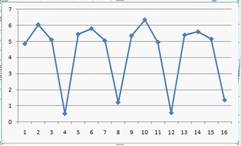 
|
Для аддитивной модели временного ряда Y = T + S + E лаг модели равен 4 и известны значения трех скорректированных сезонных компонент: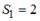 
, 
, 
, 
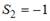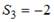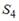равна …
|
|
|
Известно, что дисперсия временного ряда Y увеличивается с течением времени. Значит, ряд Y …
| нестационарным | |||
| стационарным | |||
| автокорреляционным | |||
| сбалансированным |
Автокорреляцией уровней ряда называется корреляционная зависимость между …
| последовательными уровнями ряда | |
| уровнями двух рядов | |
| компонентами, образующими уровни ряда | |
| факторами, формирующими уровень ряда |
Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формул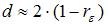е 
, где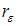 
– значение коэффициента автокорреляции остатков модели. Минимальная величина значения 
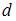будет наблюдаться при ________ автокорреляции остатков.
| положительной | |
| отрицательной | |
| нулевой | |
| бесконечно малой |
Известно, что временной ряд Y порожден случайным процессом, который по своим характеристикам является «белым шумом». Значит, ряд Y …
| стационарный | |
| нестационарный | |
| автокорреляционный | |
| сбалансированный |
Для мультипликативной модели временного ряда Y = T · S · E сумма скорректированных сезонных компонент равна …
| лагу | |
| половине лага |
Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Для аддитивной модели временного ряда для уровня y3 получено уравнение тренда T = 3,14 + 2,07t. Известны значения компонент: S3 = 1,6; E3 = –0,3. Тогда значение уровня временного ряда y3 будет равно …
|
|
|
| 10,65 | ||
| 9,35 | ||
| 1,3 | ||
| 6,51 |
