Особенность эконометрики как прикладной науки заключается в ____ существующих взаимосвязей социально-экономических показателей и систем

Для эконометрической модели линейного уравнения множественной регрессии вида 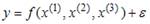построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3) – независимые переменные):

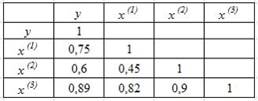
Количество пар коллинеарных независимых переменных в данной модели равно …

В эконометрической модели линейного уравнения множественной регрессии 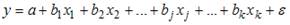величина параметра а характеризует среднее по совокупности значение зависимой переменной, при значениях ___, равных 0.

		xj
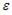		y
		a

Для регрессионной модели парной регрессии рассчитано значение коэффициента детерминации 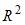. Тогда долю остаточной дисперсии зависимой переменной характеризует величина …

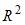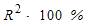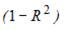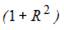Если параметр эконометрической модели является статистически значимым, то отвергается статистическая гипотеза о том, что его значение …

Проверку статистической значимости построенной эконометрической модели на основе F-критерия осуществляют с использованием …

Для оценки параметров эконометрической модели линейного уравнения регрессии вида 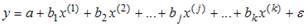используется метод наименьших квадратов (МНК), при этом выдвигаются предпосылки относительно величины …

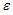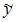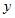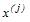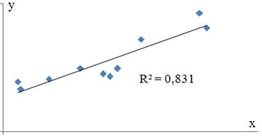
Для регрессионной модели парной регрессии рассчитано значение коэффициента детерминации 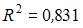(см. рис.).