Ещё больше информации даёт сервис Регрессия из Пакета анализа Excel. Для его запуска надо щелкнуть в Меню Excel 2003 и более ранних версий Сервис – Анализ данных – Регрессия. (Если Анализ данных в меню Сервиса не появится, щелкните На д стройки и установите флажок Пакет анализа). В Excel 2007 и 2010 Пакет анализа вызывается в разделе Меню Данные. Если Анализ данных не виден, установить его: Файл – Параметры – Надстройки – Параметры Excel применить – Пакет анализа. Укажите диапазоны ячеек Y и X и на какой лист выводить результаты – на новый или на тот же. В этом случае надо указать достаточно большой диапазон ячеек для вывода. Поставьте флажок, если выделили X и Y с заголовками.
Сервис Регрессия выводит все статистические характеристики модели с соответствующими надписями. Сервис Регрессия может применяться для линейных или линеаризованных моделей.
Оценка параметров Модели 1 с использованием сервиса Регрессия:
Таблица 4.3.
| Регрессионная статистика | ||
| Множественный R | 0,9243 | Квадратный корень из коэффициента детерминации. Для линейной модели – коэффициент корреляции |
| R-квадрат | 0,8544 | Коэффициент детерминации |
| Нормированный R-квадрат | 0,8382 | 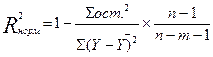
|
| Стандартная ошибка | 2,5710 | Стандартное отклонение остатков |
| Наблюдения | Количество наблюдений n |
| Дисперсионный анализ | Число степеней свободы сумм | Суммы квадратов | Дисперсия на одну степень свободы | ||
| df | SS | MS | F | Значимость F | |
| Регрессия (Y^) | 349,23 | (349,23/1=) 349,23 | 52,83 | 4,72E-05 | |
| Остаток | 59,490 | (59,49 / 9=) 6,610 | |||
| Итого (Y) | 408,72 | (Var(Y) =) 40,87 |
| Коэффи-циенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | -4,2727 | 3,7578 | -1,1370 | 0,2849 | -12,773 | 4,228 |
| X | 1,7818 | 0,2451 | 7,2686 | 4,72051E-05 | 1,227 | 2,336 |
Стандартные надписи и дополнительные пояснения позволяют быстро разобраться в таблице результатов сервиса Регрессия. Коэффициент детерминации (здесь R-квадрат), статистика Фишера F и t - статистика Стьюдента разобраны в разделе … Осталось добавить про Значимость F и Р-Значение. Соответствующие числа в таблице означают вероятности принятия неверных гипотез относительно наличия влияния всех переменных на Y (Значимость F) и каждой экзогенной переменной в отдельности (Р-Значение). В данном случае имеется одна влияющая переменная, поэтому значимости F и b совпадают. Погрешность b равна 14%, t -статистика b высокая, вероятность ошибки ничтожно мала. Погрешность a равна 88%, t -статистика низкая, и вероятность того, что a окажется больше нуля, равна 28,5% (Р -значение). В разделе Дисперсионный анализ выведены: регрессионная сумма квадратов S(Ŷ - Ŷсредн.)2, здесь равная 349,23, и соответствующая дисперсия для одной степени свободы (один х), а также сумма квадратов остатков, здесь 59,49, дисперсия остатков 6,61 и соответствующие величины для эндогенной переменной Y.
Сервис Регрессия можно применять к линеаризованным моделям, а также считая х в разных степенях в полиноме как самостоятельные экзогенные переменные, то есть сводя полиномиальную модель к модели множественной регрессии, которая рассмотрена далее. Пример: оценка параметров Модели 2 (парабола) с помощью сервиса Регрессия:
Таблица 4.4.
| Темпера-тура | Продажи | ВЫВОД ИТОГОВ | |||||
| x^2 | x | y | |||||
| Регрессионная статистика | |||||||
| Множественный R | 0,940 | ||||||
| R-квадрат | 0,884 | ||||||
| Нормированный R-квадрат | 0,871 | ||||||
| Стандартная ошибка | 2,961 | ||||||
| Наблюдения | |||||||
| Дисперсионный анализ | |||||||
| df | SS | MS | F | ||||
| Регрессия | 68,7 | ||||||
| Остаток | 157,8 | 8,7 | |||||
| Итого | |||||||
| .... | .... | .... | |||||
| Коэффици- енты | СKO | t | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 9,1942 | 1,7674 | 5,2020 | 0,0001 | 5,48 | 12,90 |
| x^2 | 0,0756 | 0,0198 | 3,8235 | 0,0012 | 0,034 | 0,117 |
| x | -0,3287 | 0,4095 | -0,8025 | 0,4327 | -1,189 | 0,531 |
 2015-05-18
2015-05-18 587
587








