Методом Монте-Карло

При работе на компьютере проще многократно проделать простые вычисления, чем один раз решить сложную аналитическую задачу. Поэтому для исследования стохастических моделей удобен метод Монте-Карло, позволяющий, в частности, оценивать погрешности параметров сложных моделей. Основные этапы реализации метода Монте-Карло:

1. Построение модели с “идеальными” параметрами.

2. Изменение значений переменных случайным образом в соответствии с дисперсией и законом распределения.

3. Расчет по проверяемой методике и сохранение параметров модели.

4. Возврат к п.2.

Пункты 2 и 3 выполняются заданное число раз – десятки, сотни, тысячи. В результате накапливаются массивы параметров, которые можно статистически обработать и установить надежность их оценок. В принципе, это можно сделать по аналитическим формулам дисперсионного анализа, но для сложной системы с внутренними связями такие расчеты становятся сложными и неустойчивыми.

В качестве примера используем эконометрическую модель парной регрессии, рассмотренную в предыдущем разделе. Этапы работы:

1. Задать коэффициенты линейной модели Yидеал = a + bX и стандартное отклонение остатков (Sост). В данном случае a= - 4,27, b= 1,78, Sост =2,44. Полученные результаты представлены в таблице 5.1. в столбце Yидеал.

Таблица 5.1.

X	Y	Yидеал	Yимит.	Ŷ	остатки
		13,55	13,55	13,13	0,42
		15,33	13,50	14,91	-1,41
		17,11	15,28	16,68	-1,4
		18,89	18,28	18,46	-0,18
		20,67	21,77	20,24	1,53
		22,45	23,55	22,01	1,54
		24,24	25,34	23,79	1,55
		26,02	25,65	25,56	0,09
		27,8	23,53	27,34	-3,81
		29,58	34,34	29,11	5,23
		31,36	27,34	30,89	-3,55
				48,48

2. Ввести в ячейки формулы и функции для расчета коэффициента детерминации R ², коэффициента автокорреляции остатков Rавт и статистики Дарбина-Уотсона DW = 2(1- Rавт), дисперсий остатков по первой и второй половинам диапазона и теста Голдфелда-Квандта GQ=МАКС(ДИСП1; ДИСП2)/МИН(ДИСП1; ДИСП2); кроме того, в данном примере вычисляется прогнозное значение для Х =30. Y(30), GQ и DW размещаются в той же строке таблицы Excel, что и коэффициенты b и a, что упрощает их сохранение.

3. Расчёт параметров модели с использованием функции ЛИНЕЙН.

b	a	Y(30)	GQ	DW
1,77	-4,62	48,48	8,05	3,11
0,25	3,94
0,84	2,70		Автокорреляция	-0,55
47,53			Дисп.ост.1	1,76
346,88	65,68		Дисп.ост.2	14,20

4. Сохранение в таблице Excel вычисленных параметров модели (сотни и тысячи имитаций) и статистическая обработка. В Таблице представлена часть массива результатов. Вычислено среднее значение каждого параметра, что позволяет оценить несмещённость, стандартное отклонение и относительную погрешность.

	b	a	Y(30)	GQ	DW
	0,95	7,60	36,22	3,88	4,11
	1,69	-3,91	46,91	1,40	3,31
	1,71	-3,55	47,90	9,47	2,69
	2,08	-10,59	51,70	1,55	3,34
	1,74	-5,20	47,14	1,93	2,86
	2,08	-8,47	53,85	7,99	2,25
Среднее	1,78	-4,42	48,96	4,37	3,09
СКО	0,2	3,14	3,113	3,52	0,64
%	11,4	71,2	6,358	80,58	20,82

В представленных таблицах не предусмотрено сохранение коэффициента детерминации, вычисляемого функцией ЛИНЕЙН. Включите его в рассмотрение.

Процедура и программный модуль для создания имитаций и сохранения результатов, а также упрощенная технология создания имитаций, позволяющая обойтись без программирования, представлены в Приложении 1.

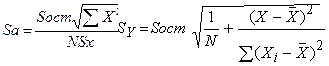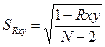5. После завершения набора результатов (не меньше 100 циклов) вычислите стандартные отклонения a, b, Y(30), GQ, DW, Rxy, сравните полученные значения с вычисленными по аналитическим формулам

6. Постройте корреляционные графики a(b), a(R²), b(R²).

7. Постройте гистограммы частотных распределений a, b, R², Y(30), DW, GQ. Для этого введите в таблицу Excel границы интервалов значений параметров (карманы) и запустите Сервис (или Данные) – Анализ данных – Гистограмма.

Исследования сравнительно простой модели – парной линейной регрессии – приводят к интересным результатам.

1. На рисунках представлены графики частотных распределений DW и GQ. Тесты показывают наличие автокорреляции для 7,5 % имитаций и гетероскедастичности для 8,5 % имитаций, причём график GQ имеет длинный хвост. Имитации создавались на основе нормального распределения возмущений, значит, автокорреляцию и гетероскедастичность можно обнаружить, если для них нет никаких предпосылок.

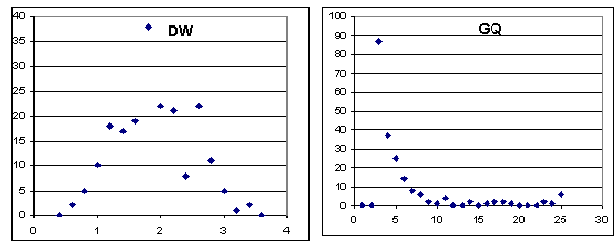
Рис.5.1.

2. В данном случае гипотеза a = 0 является приемлемой. Одна серия испытаний проведена с исключением a из модели, другая – без исключения. При ислючении aSb уменьшается втрое, а СКО Ŷпрогн(30) вдвое, но появляется систематическая погрешность (смещение).

	b	a	Ŷпрогн(30)
Среднее	1,509	0,000	45,26
СКО	0,053	0,000	1,6
СКО /среднее %	3,536		3,535

Похожие результаты были получены и при исследовании нелинейной зависимости Ŷ = a + bX + cX². При исключении слагаемого с коэффициентом b, имеющим погрешность 157%, погрешности a, c и Ŷ(30) уменьшились вдвое, но появилось смещение Ŷ(30) примерно на 10%.

4. Обработка расчетов методом Монте-Карло показала правомерность расчета погрешности точечной оценки прогноза Ŷ по формуле

S²(Ŷ)=(Sa)² + X²(Sb)²+2XCov(a,b).

Особый интерес представляет полученный коэффициент корреляции a и b, равный -0,98, что неудивительно, т.к. a = Yср – bXср. Из этого следует важнейший вывод: погрешность прогнозного значения Ŷ меньше относительных погрешностей a и b, и вдали от средних X и Y близка к разности погрешностей слагаемых в уравнении регрессии:

S(Ŷпрог) =| Sb * Xпрог– Sa |, здесь 0,2*30 – 3,14 = 2,86

что совпадает с результатами расчетов по формуле (=2,92) и методом Монте-Карло (=3,11).