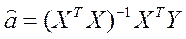Получим

(2.6.3)

Оценки, полученные с помощью МНК, являются случайными величинами, так как представляют собой линейную комбинацию случайных величин у₁, у₂, … у_n.

При выполнении предпосылок множественного регрессионного анализа оценка метода наименьших квадратов 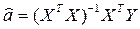является эффективной, то есть обладает наименьшей дисперсией в классе линейных несмещенных оценок.

Преобразуем вектор оценок (2.6.3) с учетом (2.6.2)

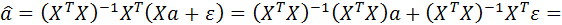
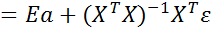
или

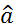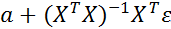= , (2.6.4)

то есть оценки параметров (2.6.3), найденные по выборке, будут содержать случайные ошибки.

Покажем, что математическое ожидание оценки 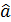равно оцениваемому параметру :

,

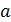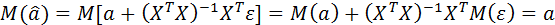так как 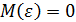. Таким образом, очевидно, что вектор 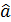есть несмещенная оценка вектора параметров .

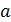Вариации оценок параметров будут в конечном счете определять точность уравнения множественной регрессии. Для их измерения в многомерном регрессионном анализе рассматривают так называемую ковариационную матрицу оценок параметров :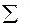

=

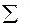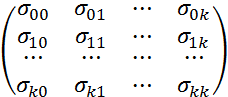
где 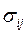- ковариации оценок параметров 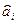и 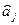. Ковариация двух переменных определяется как математическое ожидание произведения отклонений этих переменных от их математических ожиданий. Поэтому

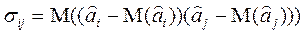(2.6.5)

Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных.

В силу того, что оценки 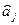, полученные методом наименьших квадратов, являются несмещенными оценками параметров 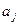, т. е. 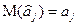, выражение (2.6.5) примет вид:

.

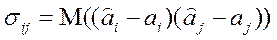Рассматривая ковариационную матрицу 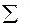, легко заметить, что на ее главной диагонали находятся дисперсии оценок параметров регрессии, так как

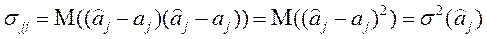. (2.6.6)

В матричном виде ковариационная матрица вектора оценок параметров 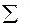имеет вид:

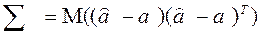
(в этом легко убедиться, перемножив векторы 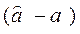и ).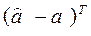

Учитывая (2.6.4), преобразуем это выражение:

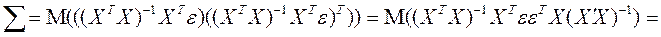
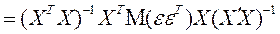(2.6.7)

ибо элементы матрицы Х – неслучайные величины.

Матрица 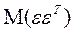представляет собой ковариационную матрицу вектора возмущений

,

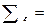
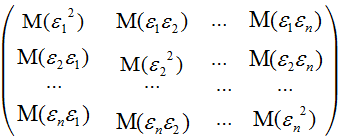в которой все элементы, не лежащие на главной диагонали, равны нулю в силу предпосылки о некоррелированности возмущени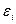й и 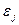между собой, а все элементы, лежащие на главной диагонали, в силу предпосылок регрессионного анализа равны одной и той же дисперсии :

.

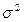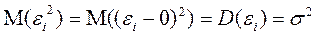Поэтому матрица

,

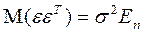где 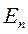- единичная матрица n -го порядка. Следовательно, в силу (2.6.7) ковариационная матрица вектора оценок параметров:

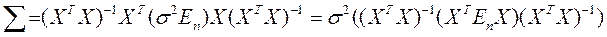
или 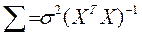(2.6.8)

Итак, с помощью обратной матрицы 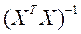определяется не только сам вектор 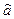оценок параметров, но и дисперсии и ковариации его компонент.

Прогноз по модели множественной линейной регрессии для вектора переменных 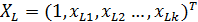составит

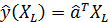(2.6.9)

Дисперсия ошибки прогноза определяется по формуле

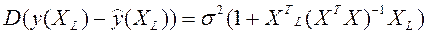. (2.6.10)

В качестве оценки 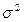используется

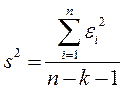. (2.6.11)

Тогда оценка дисперсии ошибки прогноза

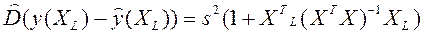(2.6.10 а)

Качество всей модели в целом определяется по критерию Фишера

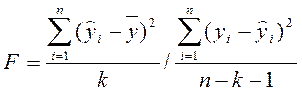. (2.6.12)

Если 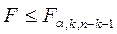, то уравнение регрессии в целом незначимо.

Здесь 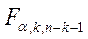- табличное значение критерия Фишера с k и n-k-1 степенями свободы уровня значимости .

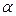Может быть рассчитан коэффициент детерминации, отражающий долю объясненной факторами дисперсии в общей дисперсии

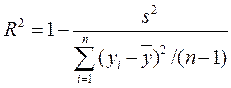. (2.6.13)

Правило проверки статистической значимости оценок 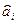(i=0,…,k) основывается на проверке статистической гипотезы

Н₀: .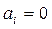

Для этого вычисляется статистика

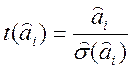, (2.6.14)

которая при выполнении гипотезы Н₀ распределена по закону Стьюдента с n-k-1 степенями свободы.

Если 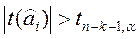, гипотезу Н₀ следует отклонить и признать коэффициент 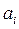статистически значимым. В противном случае следует признать 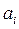статистически незначимым и переменную X_i исключить из регрессионной модели.

2.7. НЕКОТОРЫЕ ВОПРОСЫ ПРАКТИЧЕСКОГО ПРИМЕНЕНИЯ

РЕГРЕССИОННЫХ МОДЕЛЕЙ

Ранее нами была изучена классическая линейная модель множественной регрессии. Однако мы не касались некоторых проблем, связанных с практическим использованием модели множественной регрессии. К их числу относится мультиколлинеарность.

Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных. Мультиколлинеарность может проявляться в функциональной и стохастической формах.

При функциональной форме мультиколлинеарности по крайней мере одна из парных связей между объясняющими переменными является линейной функциональной зависимостью. В этом случае матрица Х^TX особенная, так как содержит линейно зависимые векторы-столбцы и ее определитель равен нулю. Это приводит к невозможности решения соответствующей системы уравнений и получения оценок параметров регрессионной модели.

Однако в экономических исследованиях мультиколлинеарность чаще всего проявляется в стохастической форме, когда между хотя бы двумя объясняющими переменными существует тесная корреляционная связь. Матрица Х^TX в этом случае является неособенной, но ее определитель очень мал. В результате получаются значительные дисперсии оценок коэффициентов регрессии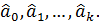

Наличие мультиколлинеарности системы объясняющих переменных можно статистически проверить по тесту Глобера – Феррара.

При отсутствии мультиколлинеарности статистика

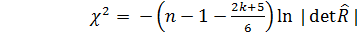, (2.7.1)

где 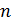– объем выборки;

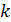- количество объясняющих переменных;

det 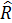– определитель выборочной корреляционной матрицы объясняющих переменных ,

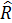имеет 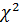- распределение с k(k-1)/2 степенями свободы.

Вычисленное значение 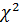сравнивается с табличным значением уровня значимости α для k(k-1)/2 степеней свободы.

Одним из методов снижения мультиколлинеарности системы объясняющих переменных X₁, X₂, …, X_k является выявление пар переменных с высокими коэффициентами корреляции (более 0,8). При этом одну из таких переменных исключают из рассмотрения. Какую из двух переменных удалить решают на основании экономических соображений или оставляют ту, которая имеет более высокий коэффициент корреляции с зависимой переменной.

Полезно также находить множественные коэффициенты корреляции между одной объясняющей переменной и некоторой группой из них.

Множественный коэффициент корреляции служит мерой линейной зависимости между случайной величиной Х_i и некоторым набором других случайных величин X₁, X₂, X₃, …,X_i-1,X_i+1,… X_k.

Множественный коэффициент корреляции 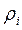определяется как обычный коэффициент парной корреляции между Х_i и Х_i^*, где Х_i^* − наилучшее линейное приближение Х_i случайными величинами X₁, X₂, X₃, …,X_i-1,X_i+1,… X_k.

Чем ближе значения коэффициента множественной корреляции к единице, тем лучше приближение случайной величины Х_i линейной комбинацией случайных величин X₁, X₂, X₃, …,X_i-1,X_i+1,… X_k.

Множественный коэффициент корреляции выражается через элементы корреляционной матрицы следующим образом:

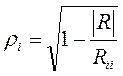, (2.7.2)

где ǀRǀ – определитель корреляционной матрицы R;

R_ii – алгебраическое дополнение элемента r_ii.

Если 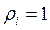, то величина Х_i представляет собой линейную комбинацию случайных величин X₁, X₂, X₃, …,X_i-1,X_i+1,… X_k.

С другой стороны, 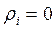только тогда, когда Х_i не коррелированна ни с одной из случайных величин X₁, X₂, X₃, …,X_i-1,X_i+1,… X_k.

В качестве выборочной оценки коэффициента множественной корреляции используется выражение

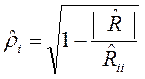(2.7.3)

Наличие высокого множественного коэффициента корреляции (более 0,8) также свидетельствует о мультиколлинеарности.

Еще одним из методов уменьшения мультиколлинеарности является использование пошаговых процедур отбора наиболее информативных переменных с использованием скорректированного коэффициента детерминации.

Недостатком коэффициента детерминации R² для выбора наилучшего уравнения регрессии является то, что он всегда увеличивается при добавлении новых переменных в регрессионную модель. Поэтому целесообразно использовать скорректированный коэффициент детерминации 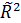, определяемый по формуле

.

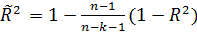В отличие от R² скорректированный коэффициент 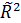может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенного влияния на зависимую переменную.

На первом шаге рассматривается лишь одна объясняющая переменная, имеющая с зависимой переменной Y наибольший коэффициент корреляции (детерминации). На втором шаге включается в регрессию новая объясняющая переменная, которая вместе с первоначальной дает наиболее высокий скорректированный коэффициент детерминации с Y ит. д.

Процедура введения новых переменных продолжается до тех пор, пока будет увеличиваться скорректированный коэффициент детерминации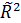

2.8. ЛИНЕЙНЫЕ РЕГРЕССИОННЫЕ МОДЕЛИ С ПЕРЕМЕННОЙ СТРУКТУРОЙ. ФИКТИВНЫЕ ПЕРЕМЕННЫЕ

До сих пор мы рассматривали регрессионную модель, в которой в качестве объясняющих переменных выступали количественные переменные (производительность труда, себестоимость продукции, доход и т. п.). Однако на практике достаточно часто возникает необходимость исследования влияния качественных признаков, имеющих два или несколько уровней (градаций). К числу таких признаков можно отнести пол (мужской, женский), образование (начальное, среднее, высшее), фактор сезонности (зима, весна, лето, осень) и т.п.

Например, нам надо изучить зависимость размера заработной платы работников Y не только от количественных факторов 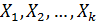, но и от качественного признака 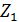, например фактора «пол работника».

В принципе можно было бы получить оценки регрессионной модели

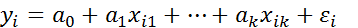(i=1,..,n) (2.8.1)

для каждого уровня качественного признака (т. е. выборочное уравнение регрессии отдельно для работников-мужчин и отдельно – для женщин), а затем изучать различия между ними.

Но есть и другой подход, позволяющий оценивать влияние количественных переменных и уровней качественных признаков с помощью одного уравнения регрессии. Этот подход связан с введением так называемых фиктивных переменных.

В качестве фиктивных переменных обычно используют дихотомические (булевы) переменные, которые принимают всего 2 значения: 0 или 1 (например, значение такой переменной Z₁ по фактору «пол»: Z₁=0 для работников-женщин и Z₁=1 для мужчин).

В этом случае первоначальная регрессионная модель (2.8.1) заработной платы изменится и примет вид

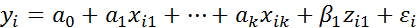(i=1,..,n) (2.8.2)

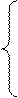1, если i -й работник мужского пола;

где =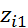

0, если i-й работник женского пола.

Таким образом, принимая модель (2.8.2), мы считаем, что средняя заработная плата у мужчин на 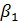*1= 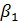выше, чем у женщин, при неизменных значениях других параметров модели. А проверяя гипотезу H₀: 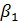= 0, мы можем установить существенность влияния фактора «пол» на размер заработной платы работника.

Следует отметить, что в принципе качественное различие можно формализовать с помощью любой переменной, принимающей два разных значения, не обязательно 0 или 1. Однако в эконометрической практике почти всегда используются фиктивные переменные типа «0-1», так как при этом интерпретация полученных результатов выглядит наиболее просто.

Если рассматриваемый качественный признак имеет несколько (k) уровней (градаций), то в принципе можно было бы ввести в регрессионную модель дискретную переменную, принимающую такое же количество значений (например, при исследовании зависимости заработной платы Y от уровня образования Z можно рассматривать k=3 значения: z_i1=1 при наличии начального образования, z_i1=2 – среднего и z_i1=3 при наличии высшего образования). Однако обычно так не поступают из-за трудности содержательной интерпретации соответствующих коэффициентов регрессии, а вводят k-1 бинарных переменных.

В рассматриваемом примере для учета факторов образования можно в регрессионную модель (2.8.2) ввести k-1=3-1=2 бинарные переменные Z₁ и Z₂:

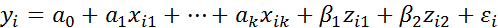(2.8.3)

1, если i- й работник имеет высшее образование;

где =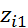

0 во всех остальных случаях.

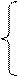1, если i- й работник имеет среднее образование;

=

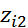0 во всех остальных случаях.

Третьей бинарной переменной очевидно не требуется, если i- й работник имеет начальное образование, это будет отражено парой значений 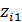=0, 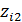=0. Более того, вводить третью бинарную переменную Z₃ со значениями 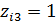, если i- й работник имеет начальное образование; 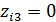- в остальных случаях, нельзя, так как при этом для любого i- го работника

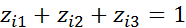
Это означает линейную зависимость столбцов общей матрицы X, т.е. мы оказались бы в условиях мультиколлинеарности в функциональной форме и как следствие – невозможности получения оценок методом наименьших квадратов.