Тест Гольдфельда-Квандта на гомоскедастичность

Этот тест применяется в том случае, если ошибки регрессии можно считать нормально распределенными случайными величинами.

Предположим, что средние квадратичные отклонения возмущений 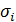пропорциональны значениям объясняющей переменной Х (это означает постоянство часто встречающегося на практике относительного а не абсолютного, как в классической модели, разброса возмущений 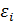регрессионной модели).

Упорядочим n наблюдений в порядке возрастания значений Х и выберем m первых и m последних наблюдений.

В этом случае гипотеза о гомоскедастичности будет равносильна тому, что значения 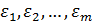и 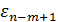, , 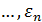то есть остатки 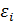регрессии первых и последних m наблюдений, представляют собой выборочные наблюдения нормально распределенных случайных величин, имеющих одинаковые дисперсии.

Гипотеза о равенстве дисперсий двух нормально распределенных совокупностей проверяется с помощью критерия Фишера.

Нулевая гипотеза о равенстве дисперсий двух наборов по m наблюдений, то есть гипотеза о гомоскедастичности отвергается, если

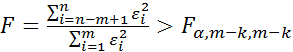, (2.10.6)

где k – число независимых переменных модели.

Мощность теста, то есть вероятность отвергнуть гипотезу о гомоскедастичности, когда действительно гомоскедастичности нет, оказывается максимальной, если выбирать m порядка n/3.

Пример. По данным n=150 наблюдений о доходе индивидуума Y, уровне его образования X₁ и возрасте X₂ выяснить, можно ли считать на уровне значимости α=0,05 линейную регрессионную модель Y по X₁ и X₂ гомоскедастичной.

Возьмем по m=n/3=150/3=50 значений доходов лиц с наименьшим и наибольшим уровнем образования X₁.

Вычислим суммы квадратов остатков

= .

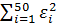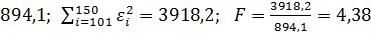По таблице распределения Фишера находим, что

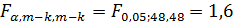
Это означает, что гипотеза о гомоскедастичности должна быть отвергнута.