Метод наименьших квадратов. Предположим, что функция регрессии переменной Y на X линейна

Предположим, что функция регрессии переменной Y на X линейна:

y = M (Y / X = x) = a x + b. (2.3)

В этом случае говорят о линейной регрессии. Тогда модель парной линейной регрессии можно представить в виде

Y = aX + b + e, (2.4)

где a, b – теоретические параметры (теоретические коэффициенты)

регрессии, e – случайное возмущение.

Модель линейной регрессии является наиболее распространенным (и простым) видом зависимости между экономическими переменными. Построенная линейная модель может служить начальной точкой эконометрического анализа. Кроме того, линейная регрессия находит широкое применение в эконометрике в силу четкой экономической интерпретации ее параметров.

Знак коэффициента регрессии a в модели указывает направление связи между переменными X и Y: если a > 0, связь прямая; если a < 0, то связь обратная. Величина коэффициента регрессии a показывает, на какую величину в среднем изменится результирующая переменная Y, если переменная X увеличится на одну единицу своего измерения.

Формально значение параметра b в модели – это среднее значение результирующей переменной Y при X = 0. Однако здесь необходима определенная осторожность. Если переменная X не имеет и не может иметь нулевого значения, вышеуказанная трактовка параметра b теряет смысл.

Пример 2.1. Парная линейная регрессия часто используется в эконометрике при изучении зависимости потребления Y от величины дохода X.

Предположим, что функция регрессии потребления на доход (в тыс. руб.) имеет вид: y ^* = 1,5 + 0,65 x.

Коэффициент регрессии a = 0,65 характеризует склонность к потреблению. Он показывает, что из каждой тысячи рублей дохода на потребление расходуется в среднем 650 рублей.

Свободный член b = 1,5 формально показывает, что при отсутствии дохода (x = 0) потребление, тем не менее, составляет 1 500 рублей. Если данный вывод применим к отдельному индивидууму или отдельной семье (они могут жить и в долг), то он вряд ли применим, например, к экономике государства. g

Для точного описания уравнения регрессии (2.3) необходимо знать условный закон распределения зависимой переменной Y при условии, что независимая переменная X примет значение x, т.е. X = x. В статистической практике такую информацию получить, как правило, не удается. Однако у исследователя имеются статистические (или выборочные) данные (x_i, y_i), i = 1, 2, …, n, полученные в результате n независимых наблюдений над переменными X и Y. В этом случае по выборочным данным можно оценить (приближенно выразить) теоретическую функцию регрессии (2.3). Такой оценкой является выборочное уравнение регрессии

y ^* = a ^* × x + b ^*, (2.5)

где y ^* – оценка условного математического ожидания переменной Y, т.е.

функции y = M (Y / X = x);

a ^* и b ^* – оценки неизвестных параметров a и b соответственно.

Построение выборочного уравнения регрессии (2.5) сводится к нахождению его параметров a ^* и b ^*, которые могут быть найдены разными способами. Наиболее простой метод состоит в следующем. Изобразим выборочные данные (x_i, y_i), i = 1, 2, …, n, в виде точек на координатной плоскости (рис. 2.1). Такое графическое изображение статистических данных называется корреляционным полем (или диаграммой рассеяния).

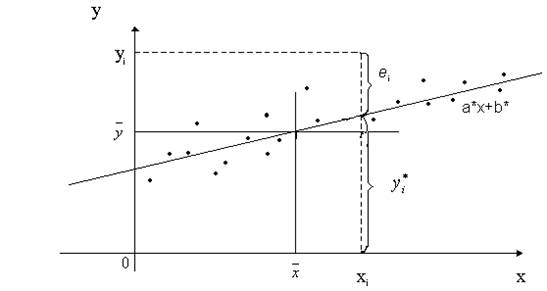
Рис.2.1. Корреляционное поле

Выберем две точки на диаграмме рассеяния и проведем через них прямую линию. Далее по графику нетрудно определить коэффициенты этой прямой. Очевидно, подобным образом можно построить много различных прямых, однако непонятно, какая из них наилучшим образом отражает зависимость между переменными X и Y.

Самый распространенный и теоретически обоснованный подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Этот метод является также наиболее простым с вычислительной точки зрения. Кроме того, оценки, полученные МНК, при определенных предпосылках, обладают рядом оптимальных свойств.

Суть МНК нахождения неизвестных параметров a ^* и b ^* состоит в том, чтобы сумма квадратов отклонений выборочных значений y_i от значений y_i ^*, найденных по уравнению регрессии (2.5), была минимальной:

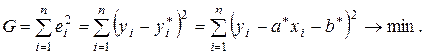(2.6)

Необходимым условием существования минимума функции двух переменных G = G (a ^*, b ^*) является равенство нулю ее частных производных:

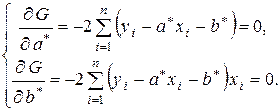
В уравнениях системы раскроем скобки и после несложных преобразований получим так называемую систему нормальных уравнений для определения неизвестных параметров линейной регрессии:

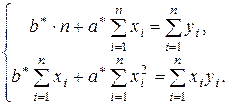
Решение системы можно найти достаточно легко методом последовательного исключения неизвестных (или методом Крамера):

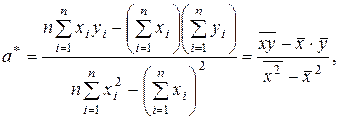(2.7)

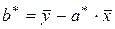. (2.8)

В соотношениях (2.7) и (2.8) соответствующие средние определяются по формулам:

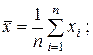(2.9) 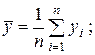(2.10)

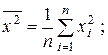(2.11) 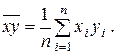(2.12)

Подставляя значение b ^*из равенства (2.8) в уравнение регрессии (2.5), получим

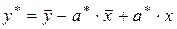
или

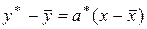. (2.13)

Из полученного уравнения регрессии (2.13) видно, что линия регрессии проходит через точку 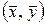(см. рис. 2.1).

Пример 2.2. Изучается зависимость между величиной потребительских расходов Y (усл. ед.) и доходом X (усл. ед.) на одного члена семьи. Для этого помесячно в течение года отобрана выборка объема n = 12, результаты которой приведены в следующей таблице.

Таблица 2.1

i

xi

yi

Необходимо:

а) определить вид зависимости между X и Y и записать ее в виде модели;

б) по МНК оценить параметры уравнения регрессии Y на X и построить выборочное уравнение регрессии;

в) дать экономическую интерпретацию полученным оценкам параметров уравнения регрессии.

Решение. а) Для определения вида зависимости между X и Y построим корреляционное поле (рис. 2.2).

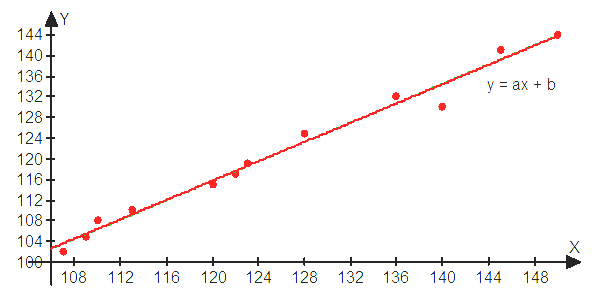
Рис. 2.2. Корреляционное поле и прямая регрессии

Поскольку точки на корреляционном поле располагаются около некоторой прямой y = ax + b, томожно предположить наличие линейной регрессионной зависимости между переменными X и Y:

Y = aX +b + e,

где a, b – неизвестные параметры, e – случайное возмущение.

б) Для наглядности вычислений построим табл. 2.2.

Таблица 2.2

i	xi	yi		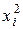	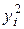xi yi
			11 449	10 404	10 914
			11 881	11 025	11 445
			12 100	11 664	11 880
			12 769	12 100	12 430
			14 400	13 225	13 800
			14 884	13 689	14 274
			15 129	14 161	14 637
			16 384	15 625	16 000
			18 496	17 424	17 952
			19 600	16 900	18 200
			21 025	19 881	20 445
			22 500	20 736	21 600
S	1 503	1 448	190 617	176 834	183 577

Вычислим по формулам (2.9) – (2.12) все необходимые средние:

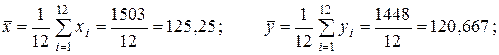
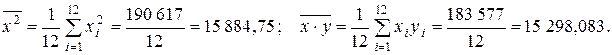
Согласно МНК по формулам (2.8) и (2.9) находим

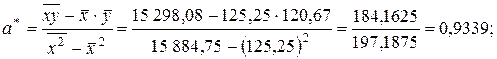
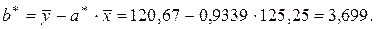
Таким образом, уравнение парной линейной регрессии имеет вид:

y ^* = 0,9339 x + 3,699. (2.14)

Изобразим данную прямую на корреляционном поле (рис. 2.2).

в) Коэффициент a ^*» 0,934 полученного уравнения регрессии показывает, что увеличение дохода (на одного человека) на 1 усл. ед. влечет увеличение расходов примерно на 0,934 усл. ед. Значение b ^*» 3,7 говорит о том, что при нулевом доходе расходы составят в среднем примерно 3,7 усл. ед. Этот факт можно объяснить для отдельной семьи (она может тратить накопленные или одолженные средства), но для совокупности семей он теряет смысл. g