Основные предпосылки регрессионного анализа

1 ⁰. В модели (2.4) парной линейной регрессии возмущение e есть случайная величина, объясняющая переменная X – величина неслучайная.

2 ⁰. Математическое ожидание случайного возмущения e _i равно нулю:

M (e _i) = 0 для всех наблюдений 1 ).

Данное условие означает, что хотя в каждом конкретном наблюдении случайное отклонение может быть положительным или отрицательным, оно не должно иметь систематического смещения. Другими словами, случайное возмущение в среднем не должно оказывать влияния на результирующую переменную.

3 ⁰. Дисперсия случайных возмущений постоянна:

D (e _i) = s ² для всех наблюдений.

Выполнение данного условия называется гомоскедастичностью (постоянством дисперсии) возмущений, невыполнение – гетероскедастичностью (непостоянством дисперсии) возмущений.

4 ⁰. Возмущения e _i и e _j (i ¹ j) не коррелированны:

cov (e _i , e _j) = 0 для всех наблюдений.

Если данное условие выполняется, то говорят об отсутствии автокорреляции возмущений, в противном случае – о ее наличии.

5 ⁰. Возмущение e _i есть нормально распределенная случайная величина:

e _i ~ N (0, s) для всех наблюдений.

Замечание 2.1. При выполнении предпосылки 5 ⁰ условие 4 ⁰ некоррелированности возмущений e_i и e_j (i ¹ j) равносильно их независимости. 3

Теорема 2.1 (Гаусса – Маркова). Если выполнены предпосылки 1 ⁰ – 4 ⁰, то МНК-оценки a ^* и b ^* обладают следующими свойствами:

· оценки являются несмещенными, т.е. M (a ^*) = a, M (b ^*) = b;

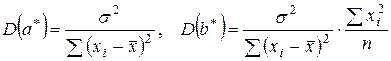· , (2.16)

где s ² – дисперсия возмущений;

·оценки состоятельны: a ^* ® a, b ^* ® b по вероятности при n ® ¥;

· оценки эффективны, т.е. они имеют наименьшие дисперсии по сравнению с любыми другими несмещенными оценками, линейными относительно величин y_i, i = 1, 2, …, n.

Оценкой теоретического уравнения регрессии (2.3) является выборочное уравнение регрессии (2.5), где a ^* и b ^* – МНК-оценки, найденные по формулам (2.7) и (2.8) соответственно. Воздействие случайных возмущений 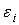в модели (2.15) определяется с помощью дисперсии возмущений или остаточной дисперсии s ² = D (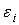). Так как случайные возмущения 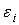по выборке определены быть не могут, они заменяются на отклонения 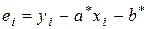фактических значений y_i переменной Y от оцененных с помощью уравнения регрессии (2.5). Тогда несмещенной оценкой дисперсии возмущений (остаточной дисперсии) s ² является выборочная остаточная дисперсия

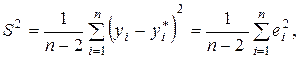(2.17)

где y_i ^* = a ^*× x_i + b ^* – значение зависимой переменной Y, найденное по

выборочному уравнению регрессии (2.5);

e_i = y_i – y_i ^* – выборочная оценка возмущения e _i или остаток регрессии.

Оценками дисперсий выборочных коэффициентов регрессии a ^* и b ^*, в силу (2.16) и (2.17), являются величины

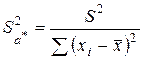, (2.18)

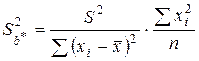. (2.19)

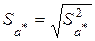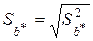
Выборочные стандартные отклонения и выборочных коэффициентов регрессии a ^*и b ^* соответственно часто называют стандартными ошибками коэффициентов регрессии.

Пример 2.3. По данным примера 2.2 вычислить выборочную остаточную дисперсию и стандартные ошибки коэффициентов регрессии.

Решение. Для вычисления выборочной остаточной дисперсии S ² составим следующую таблицу:

Таблица 2.3

i	xi	yi	yi * = 0,9339 xi + 3,699	ei = yi – yi *	ei 2
			103,63	–1,63	2,66
			105,49	–0,49	0,24
			106,43	1,57	2,46
			109,23	0,77	0,59
			115,77	–0,77	0,59
			117,63	–0,63	0,40
			118,57	0,43	0,18
			123,24	1,76	3,10
			130,71	1,29	1,66
			134,45	–4,45	19,8
			139,11	1,89	3,57
			143,78	0,22	0,05
S			» 1448*)	» 0*)	35,3

По формуле (2.17) имеем теперь:

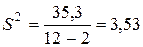, откуда .

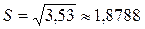В примере 2.2 найдены величины 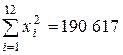и .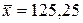

При вычислении 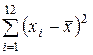воспользуемся табл. 2.2. Для этого заметим, что

,

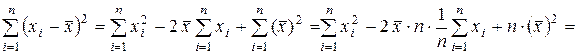
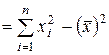поэтому

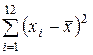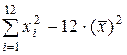= = 190 617 – 12× (125,25)² = 2 366,256.