Аналитическое выравнивание временного ряда

В эконометрике большое внимание при выделении основной тенденции временного ряда уделяется методу аналитического выравнивания (сглаживания). Этот метод основан на допущении, что исследователь может задать общий вид функции f (t), описывающей неслучайную составляющую временного ряда. В экономической практике такие функции часто называют кривыми роста. Их условно можно разделить на два класса в зависимости от того, какой тип динамики развития они отражают: кривые роста без «насыщения» и кривые роста с «насыщением».

К первому классу относятся функции, используемые для описания процессов с монотонным (или кусочно-монотонным) характером тенденции развития и отсутствием пределов роста. Эти условия справедливы для многих экономических показателей, например, для большинства показателей промышленного производства в натуральном выражении. Среди кривых роста первого класса, прежде всего, следует выделить полиномы (многочлены):

,

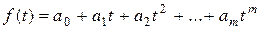где a_j (j = 0, 1, …, m) – коэффициенты и m – степень многочлена.

Коэффициенты полиномов невысоких степеней могут иметь конкретную интерпретацию в зависимости от содержания динамического ряда. Например, их можно трактовать как скорость роста (a ₁), ускорение роста (a ₂), изменение ускорения (a ₃).

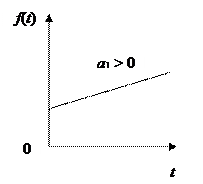
При выборе соответствующего полинома часто используют содержательный анализ (который может установить характер динамики процесса), а также визуальные наблюдения на основе графического изображения временного ряда (рис 7.2).

f (t)   а) Полином 1-го порядка f (t) = a 0 + a 1 t a 0

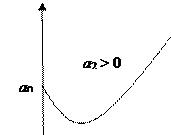t б) Полином 2-го порядка f (t) = a 0 + a 1 t + a 2 t 2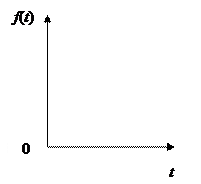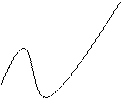

с) Полином 3-го порядка f (t) = a 0 + a 1 t + a 2 t 2 + a 3 t 3 a 0

Рис. 7.2. Полиномиальные кривые роста

Для подбора степени полинома может быть применен метод последовательных разностей. Суть этого метода состоит в вычислении разностей 1-го порядка D _t = y_t – y_{t – 1}, 2-го порядка 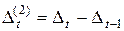, 3-го порядка 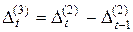и т. д. Порядок разностей, при котором они будут примерно одинаковыми, принимается за степень полинома.

К представителям кривых роста первого класса относятся также показательные(экспоненциальные) функции, для которых характерна зависимость приростов от значений самой функции. Эти кривые хорошо описывают процессы, имеющие «лавинообразный» характер, когда прирост зависит от достигнутого уровня функции.

Простая показательная (экспоненциальная) кривая имеет вид:

.

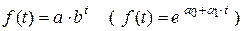Если b > 1 (a ₁ = ln b > 0), то кривая растет вместе с ростом t, и убывает, если b < 1 (a ₁ = ln b < 0) (рис. 7.3).

Параметр а (a ₀ = ln a) характеризует начальные условия развития, а параметр b – постоянный темп роста.

b < 1 a

Рис. 7.3. Показательная кривая роста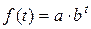

Рассмотренные выше кривые роста используются для описания процессов без «насыщения», с монотонно (или кусочно-монотонно) возрастающим или убывающим характером тенденции.

Когда процесс характеризуется «насыщением», его следует описывать при помощи кривой, имеющей отличную от нуля асимптоту. Примером такой кривой может служить модифицированная экспонента

,

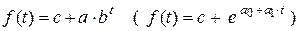где y = c – горизонтальная асимптота.

Если параметр a < 0, то асимптота находится выше кривой, если a > 0, то ниже (рис. 7.4). При решении экономических задач чаще всего приходится иметь дело с кривой, у которой a < 0, b < 1. В этом случае рост происходит с замедлением и стремится к некоторому пределу.

a > 0, b < 1 c f (t)) t

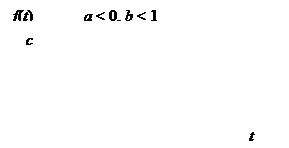Рис. 7.4. Модифицированная экспонента

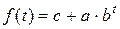
При решении экономических задач асимптоту кривой роста часто можно определить, исходя из свойств изучаемого процесса. Так, например, коэффициент использования оборудования не может превышать единицы. Иногда значение асимптоты задается экспертным путем. Например, главный инженер предприятия указывает, что производственные мощности не позволяют наращивать объемы производства выше определенного уровня. Этот уровень является тогда оценкой значения асимптоты при прогнозировании производства продукции.

Исследование динамики социальных и экономических процессов выявило довольно сильную распространенность эффекта «насыщения»: выхода на асимптоту при достижении определенных значений показателей. Если воздействие ограничивающего фактора начинает сказываться только после определенного момента (точки перегиба), до которого процесс развивался по некоторому экспоненциальному закону, то для описания такого процесса используют S -образные кривые. Наиболее известные из них – кривая Гомперца и логистическая кривая.

Уравнение кривой Гомперца имеет вид:

.

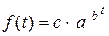Если ln a < 0, кривая имеет S -образный вид, при этом асимптота y = с проходит выше кривой. Если ln a > 0, асимптота y = с лежит ниже кривой, а сама кривая меняется монотонно: при b < 1 она монотонно убывает, а при

b > 1 – монотонно возрастает (рис. 7.5).

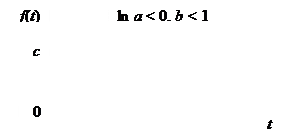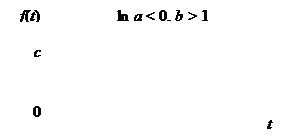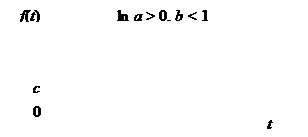Рис. 7.5. Кривая Гомперца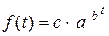

К этому же типу кривых роста с «насыщением» относится логистическая кривая

.

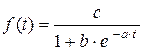Эта кривая характеризует развитие показателя во времени, когда ускоренный рост в начале периода сменяется замедляющимся темпом роста вплоть до полной остановки, что на графике соответствует отрезку кривой, параллельному оси абсцисс (рис. 7.6).

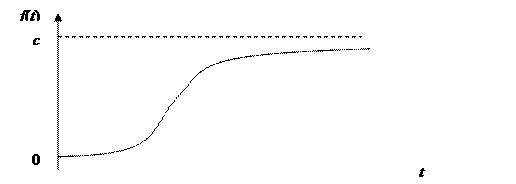Рис. 7.6. Логистическая кривая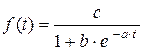

С помощью логистической кривой хорошо описывается развитие новой отрасли (нового производства). Сначала технические методы производства еще недостаточно разработаны, издержки производства высоки и спрос на рынке на данный товар еще мал, поэтому производство развивается медленно. В дальнейшем, благодаря усовершенствованию технических методов изготовления, переходу к массовому производству и увеличению емкости рынка для данного товара производство растет быстрее. Затем наступает период насыщения рынка, рост производства все более замедляется и наконец прекращается. Наступает стабилизация производства на определенном уровне.

Для оценки параметров основной тенденции чаще всего используется метод наименьших квадратов (МНК), рассмотренный в темах 2 и 3. При этом значения временного ряда y_t рассматриваются как зависимая переменная, а время t – как объясняющая переменная:

y_t = f (t) + ,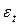

где 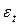– «возмущения», удовлетворяющие основным предпосылкам регрессионного анализа, приведенным в п. 3.2.

Напомним, например, что согласно МНК оценки параметров прямой 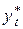= = 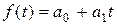находятся по формулам (2.7) и (2.8) (тема 2), в которых в качестве x_i берется t:

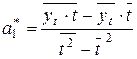, (7.7)

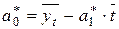, (7.8)

где

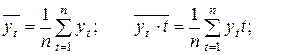(7.9)

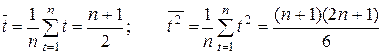. (7.10)

В двух последних соотношениях мы воспользовались тем, что значения переменной t = 1, 2, …, n образуют натуральный ряд чисел от 1 до n, и поэтому суммы 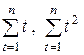можно выразить через число членов ряда n по известным формулам:

.

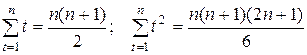Пример 7.3. По данным примера 7.1 найти уравнение неслучайной составляющей (тренда) для временного ряда y_t, полагая его линейным. Проверить значимость уравнения тренда на 5%-м уровне.

Решение. По формулам (7.9) и (7.10) рассчитаем средние

.

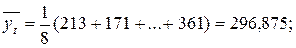
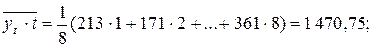
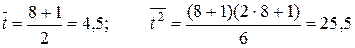Подставляя найденные средние в формулы (7.7) и (7.8), получаем:

,

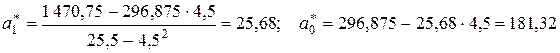откуда уравнение тренда

.

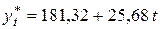На рис. 7.7 график трендовой составляющей временного ряда изображен сплошной прямой. Полученное уравнение тренда показывает, что спрос ежегодно увеличивается в среднем на 25,7 усл. ед.

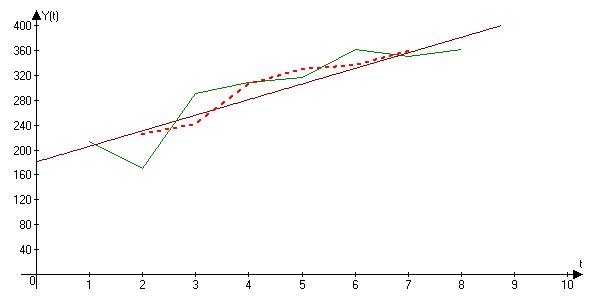
Рис.7.7. Временной ряд (сплошная ломаная), тренд (сплошная прямая)

и сглаженный ряд (пунктирная ломаная)

Проверим значимость полученного уравнения тренда по F -критерию на 5%-м уровне значимости. Для этого вычислим вначале сумму квадратов отклонений, обусловленную трендом. В силу соотношения (2.13) уравнение тренда можно записать в виде 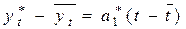. Следовательно,

.

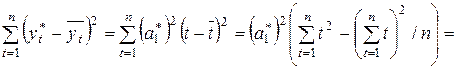
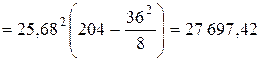Общая сумма квадратов отклонений равна

.

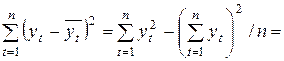
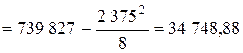Найдем по формуле (2.29) коэффициент детерминации: 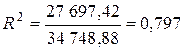, а по формуле (2.28) – значение F- статистики:

.

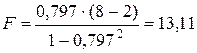По табл.3 ­ Приложения находим 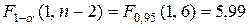. Так как F > 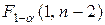(13,11 > 5,99), то уравнение тренда значимо. g

Замечание 7.1. При применении метода наименьших квадратов для оценки параметров экспоненциальной, логистической функций или функции Гомперца возникают сложности с решением получаемой системы нормальных уравнений. Поэтому предварительно, до получения соответствующей системы, прибегают к некоторым преобразованиям этих функций (например, логарифмированию и др. (см. п. 4.1)). 3