2015-05-18
213
- Упорядочить n наблюдений по мере возрастания переменной x
- Исключить из рассмотрения c центральных наблюдений, при этом
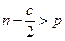, p – число оцениваемых параметров. Возможно, что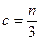 
- Определить по каждой из двух групп уравнения регрессии
- Определить остаточную сумму квадратов для каждой из групп S1 и S2, поделить большую сумму на меньшую и сравнить со значением f критерия Фишера.
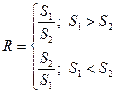
Если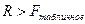 
, то присутствует гомоскедастичность.
Чем больше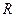 
превышает 
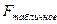, тем более нарушена предпосылка о равенстве дисперсий остатков.
Из экспериментальных расчетов, проведенных авторами метода для случая одного фактора, рекомендовано при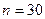 
принимать 
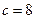, при 
, 
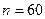, при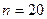 
, 
.
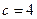Пример:
Поступление доходов в консолидированный бюджет Санкт-Петербурга
(y – млрд. руб.) в зависимости от численности работающих на крупных и средних предприятиях (x – тыс. чел.) экономики районов за 1994 г.
| № | Районы города |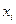 
| 
| 
| 
|
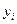
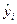
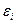
| Павловский | 4,4 | -1,0 | 5,4 | ||
| Кронштадт | 8,1 | 2,5 | 5,6 | ||
| Ломоносовский | 12,9 | 4,9 | 8,0 | ||
| Курортный | 20,8 | 16,6 | 4,2 | ||
| Петродворец | 15,5 | 19,0 | -3,5 | ||
| Пушкинский | 28,8 | 22,5 | 6,3 | ||
| Красносельский | 37,5 | 41,4 | -3,9 | ||
| Приморский | 48,7 | 53,2 | -4,5 | ||
| Колпинский | 68,6 | 66,1 | 2,5 | ||
| Фрунзенский | 104,6 | 82,6 | 22,0 | ||
| Красногвардейский | 90,5 | 88,5 | 2,0 | ||
| Василеостровский | 88,3 | 107,4 | -19,1 | ||
| Невский | 132,4 | 120,4 | 12,0 | ||
| Петроградский | 122,0 | 127,4 | -5,4 | ||
| Калининский | 99,1 | 131,0 | -31,9 | ||
| Выборгский | 114,2 | 142,7 | -28,5 | ||
| Кировский | 150,6 | 151,0 | -0,4 | ||
| Московский | 156,1 | 171,0 | -14,9 | ||
| Адмиралтейский | 209,5 | 180,5 | 29,0 | ||
| Центральный | 342,9 | 327,8 | 15,1 | ||
| Итого | 1855,5 | 1855,5 | 0,0 |
В соответствии с уравнением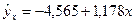 
; 
, 
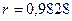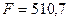найдены теоретические значения 
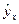и отклонения от их фактических значений 
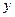, т.е. 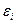. Остаточные величины 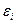обнаруживают тенденцию к росту по мере увеличения 
и .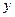
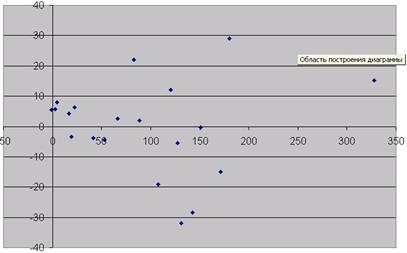
Рис.1 График остатков
, 
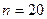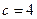
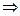в каждой крупе будет 8 наблюдений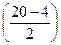 
Проверка линейной регрессии на гетероскедастичность
| Уравнения регрессии |
|
|
| 
| 
|
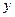
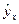
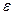
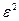
1-я группа с первыми
8 районами:
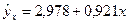
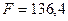
| 4,4 | 5,7 | -1,3 | 1,69 | |
| 8,1 | 8,5 | -0,4 | 0,16 | ||
| 12,9 | 10,3 | 2,6 | 6,76 | ||
| 20,8 | 19,6 | 1,2 | 1,44 | ||
| 15,5 | 21,4 | -5,9 | 34,81 | ||
| 28,8 | 24,2 | 4,6 | 21,16 | ||
| 37,5 | 38,9 | -1,4 | 1,96 | ||
| 48,7 | 48,1 | 0,6 | 0,36 | ||
| Сумма | 68,34 | ||||
2-я группа с последними
8 районами:
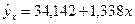
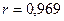
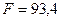
| 132,4 | 110,7 | 21,7 | 470,89 | |
| 122,0 | 118,7 | 3,3 | 10,89 | ||
| 99,1 | 122,7 | -23,6 | 556,96 | ||
| 114,2 | 136,1 | -21,9 | 479,61 | ||
| 150,6 | 145,4 | 5,2 | 27,04 | ||
| 156,1 | 168,2 | -12,1 | 146,41 | ||
| 209,5 | 178,9 | 30,6 | 936,36 | ||
| 342,9 | 346,1 | -3,2 | 10,24 | ||
| Сумма | 2638,40 |
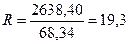, что превышает табличное значение F-критерия 4,28 при 5%-ном и 8,47 при 1%-ном уровне значимости для числа степеней свободы 6 для каждой остаточной суммы квадратов 
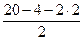, подтверждая тем самым наличие гетероскедастичности.
