Оценка достоверности выборочного уравнения регрессии и его параметров. Показатели качества модели регрессии

В корреляционно-регрессионном анализе наиболее точные характеристики связи можно получить лишь в том случае, если исследователь опирается на всю совокупность фактов и событий определенного рода, то есть если удалось провести сплошное наблюдение генеральной совокупности. Многие экономические совокупности являются бесконечными по своей численности (это совокупности фактов купли-продажи товаров, совокупность решений покупателей и т.д.), что делает сплошное наблюдение невозможным или труднореализуемым.

Если же уравнение регрессии определено по выборочным данным, то важно помнить о том, что вся интерпретация уравнения в действительности представляет собой лишь оценку реальных соотношений взаимосвязанных признаков в генеральной совокупности. Кроме того, уравнение регрессии отражает только общую закономерность для выборки. При этом каждое отдельное наблюдение подвержено воздействию случайностей. Поэтому, если выборочные характеристики связи необходимо распространить на генеральную совокупность, то следует провести статистическую оценку их достоверности или существенности.

Достоверным (существенным) показателем связи называют тот, величина которого сформировалась под действием закономерности, имеющей место в генеральной совокупности; под достоверностью в математической статистике понимают вероятность того, что значение проверяемого показателя связи не равно нулю и не включает в себя величины противоположных знаков. Недостоверный (несущественный) показатель формируется под влиянием случайных причин.

Статистическую оценку достоверности выборочных показателей связи обычно проводят в определенной последовательности. Первая процедура проводится на основе дисперсионного анализа с помощью F-критерия Фишера. Данная процедура получила название F-теста уравнения регрессии. Ее назначение - сделать вывод о правильности выбора вида взаимосвязи и дать характеристику достоверности всего уравнения регрессии в целом.

Схема F- теста:

1. Выдвигается рабочая гипотеза о равенстве генеральных дисперсий: дисперсии, воспроизведенной (σ²_регр.) уравнением регрессии, и остаточной дисперсии (σ ²_ост.), а также альтернативная ей:

Н₀: σ ²_регр. = σ ²_ост.

Н_a: σ ²_регр. ¹ σ ²_ост

1. Выбирается уровень значимости критерия .
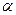2. Производится разложение общего объема вариации:

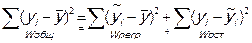Поскольку остатки определяются как: ,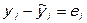

т.е. отклонения от линии регрессии по каждому наблюдению, будем обозначать остаточный объем вариации как .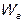

3. Определяется число степеней свободы, которое обозначается d.f. или v:

v_общ.=n-1, где n – численность выборки;

v_регр.=m (m – число параметров без условного начала). Для парной линейной регрессии v_регр.=1

v_ост..=n-m-1 Для парной линейной регрессии v_{ост .}= n-2.

4. Рассчитываются выборочные несмещенные оценки дисперсий:

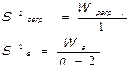
5. Определяется фактическое значение F-критерия Фишера:

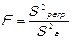6. Определяется критическое (табличное) значение критерия:

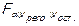
6. Делается статистический вывод:

а) Fфакт.≤ Fтабл.ÞН₀ (σ²_факт.= σ ²_ост.)

б) Fфакт.> Fтабл.ÞН_a (σ ²_факт. ¹ σ ²_ост)

7. Делается заключение о значимости уравнения в целом, в случае принятия альтернативной гипотезы при выбранном уровне вероятности суждения 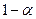, либо – о его недостоверности, если была принята нулевая гипотеза.

Если уравнение регрессии в целом значимо, то имеет смысл оценить значимость его параметров по t-критерию Стьюдента. Этот критерий применяется также для оценки значимости коэффициента парной корреляции, поскольку r – это лишь выборочная оценка генерального коэффициента корреляции .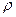

Схема t-теста:

1. Формулируются рабочая и альтернативная гипотезы:

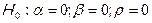
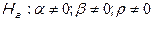Выбирается уровень значимости критерия .

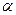2. Рассчитываются средние ошибки выборочных характеристик:

,

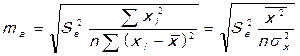где 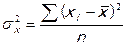– выборочная дисперсия независимой переменной х.

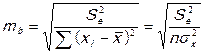
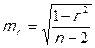
3. Определяются фактические значения t-критерия:

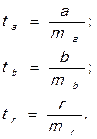
4. Определяется критическое значение:

.

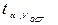5. Фактические значения сравниваются с критическим. Тестируемые параметры будут значимыми, если:

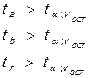
Отметим, что парной линейной модели, поскольку в модели всего один регрессор:

.

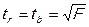Если параметры уравнения оказались значимыми, то возможна их интерпретация и распространение выводов на генеральную совокупность.

В этом случае возможна их интервальная оценка:

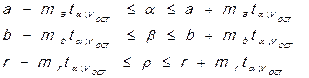
Нужно иметь ввиду, что существенные параметры регрессии не могут менять знать на противоположный. Если нижняя граница у Вас получается отрицательной, а выборочный параметр при этом – положительный, то в качестве нижней границы следует взять ноль. Аналогично для коэффициента корреляции, к тому же нужно помнить, что он изменяется в пределах от -1 до 1, соответственно предельные границы в генеральной совокупности не могут превышать по модулю единицу.

Качество оценки: коэффициент R²:

Цель регрессионного анализа состоит в объяснении поведения зависимой переменной у. В любой данной выборке у оказывается сравнительно низким в одних наблюдениях и сравнительно высоким — в других. Разброс значений у в любой выборке можно суммарно описать с помощью выборочной дисперсии Var (у).

В парном регрессионном анализе мы пытаемся объяснить поведение у путем определения регрессионной зависимости у от выбранной независимой переменной х. После построения уравнения регрессии мы можем разбить значение у_i в каждом наблюдении на две составляющих — 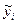и е_i: y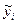_i = + e_i

Величина 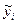— расчетное значение у в наблюдении i — это то значение, которое имел бы у при условии, что уравнение регрессии было правильным, и отсутствии случайного фактора. Это, иными словами, величина у, спрогнозированная по значению x в данном наблюдении. Остаток e_i есть расхождение между фактическим и спрогнозированным значениями величины y. Это та часть у, которую мы не можем объяснить с помощью уравнения регрессии. Используя уравнение, разложим дисперсию у:

Var (y) = Var (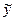 + e) = Var (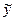) + Var(e) + 2Cov (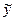, e)

Далее, Cov ( 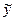,е) должна быть равна нулю. Следовательно, мы получаем:

Var (y) = Var (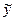) + Var (e)

Это означает, что мы можем разложить Var (у) на две части: Var (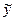) — часть, которая «объясняется» уравнением регрессии в вышеописанном смысле, и Var (е) — «необъясненную» часть.

Var (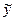)/ Var (у) — это часть дисперсии y, объясненная уравнением регрессии. Это отношение известно как коэффициент детерминации, и его обычно обозначают R ². 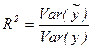, что равносильно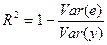

Максимальное значение коэффициента детерминации равно единице. Это происходит в том случае, когда линия регрессии точно соответствует всем наблюдениям, так что 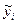= у_i для всех i и все остатки равны нулю. Тогда Var (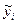) = Var (у), Var (е) = О и R² = 1.

Если в выборке отсутствует видимая связь между у и х, то коэффициент R² будет близок к нулю.

При прочих равных условиях желательно, чтобы коэффициент R² был как можно больше. В частности, мы заинтересованы в таком выборе коэффициентов а и b, чтобы максимизировать R².

3. Проблема гетероскедастичности остатков.Взвешенный метод наименьших квадратов

Вторая предпосылка МНК требует, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора остатки имеют одинаковую дисперсию. Если это условие не соблюдается, то имеет место гетероскедастичность. Наличие гомо- или гетероскедастичности можно видеть по графику зависимости остатков от теоретических значений результативного признака:

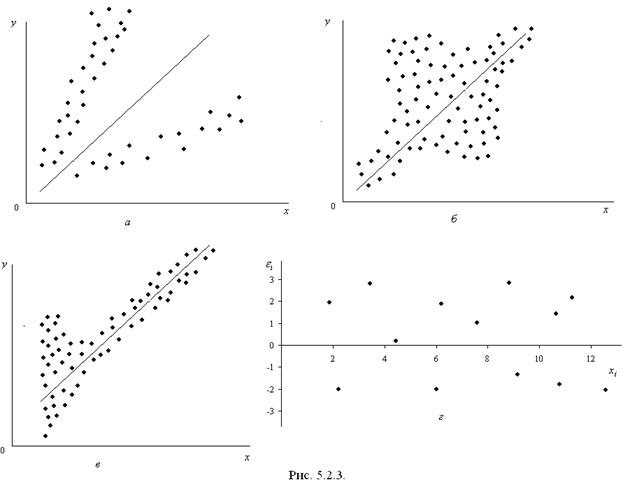
а) большая дисперсия остатков для больших значений «у» (гетероскедастичность);

б) большая дисперсия остатков для средних значений «у» (гетероскедастичность);

в) – большая дисперсия для меньших значений результата (гетероскедастичность);

г) – равная дисперсия (гомоскедастичность).

Наличие гетероскедастичности приводит к смещенным оценкам коэффициентов регрессии, а также уменьшает их эффективность. В частности, становится затруднительным использование формулы стандартной ошибки коэффициента регрессии, которая предполагает единую дисперсию остатков.

Для множественной регрессии данный вид графиков является наиболее приемлемым визуальным способом изучения гомо- или гетероскедастичности. Однако, чтобы убедиться в наличии этих качеств, обычно не ограничиваются визуальной проверкой гетероскедастичности, а проводят также ее количественное подтверждение. При малом объеме выборки, что характерно для эконометрических исследований для этих целей используется метод Гольдфельда –Квандта, который включает в себя следующие шаги:

1. Упорядочение наблюдений по мере возрастания фактора х.

2. Исключение из наблюдений нескольких центральных наблюдений (С). При этом должно выполняться условие, что (N – С)/2 должно быть больше р – число параметров в модели.

3. Распределение оставшихся наблюдений на две равные группы с малыми и большими значениями факторного признака.

4. Решение уравнения регрессии для каждой группы (имеем два уравнения).

5. Определение остаточной суммы квадратов отклонений для каждой группы и определение их отношения (отношение большей к меньшей). Сравнение этого отношения с табличным значением критерия Фишера (d f = n - C – 2p/2). Если это отношение меньше табличного значения F- критерия, то мы имеем гомоскедастичные остатки. Чем больше это отношение превышает табличное, тем больше нарушена предпосылка о равенстве дисперсий остаточных величин.

Одной из основных гипотез МНК является предположение о равенстве дисперсий отклонений еi, т.е. их разброс вокруг среднего (нулевого) значения ряда должен быть величиной стабильной. Это свойство называется гомоскедастичностью. На практике дисперсии отклонений достаточно часто неодинаковы, то есть наблюдается гетероскедастичность. Это может быть следствием разных причин. Например, возможны ошибки в исходных данных. Случайные неточности в исходной информации, такие как ошибки в порядке чисел, могут оказать ощутимое влияние на результаты. Часто больший разброс отклонений єi, наблюдается при больших значениях зависимой переменной (переменных). Если в данных содержится значительная ошибка, то, естественно, большим будет и отклонение модельного значения, рассчитанного по ошибочным данным. Для того, чтобы избавиться от этой ошибки нам нужно уменьшить вклад этих данных в результаты расчетов, задать для них меньший вес, чем для всех остальных. Эта идея реализована во взвешенном МНК.

Пусть на первом этапе оценена линейная регрессионная модель с помощью обычного МНК. Предположим, что остатки еi независимы между собой, но имеют разные дисперсии (поскольку теоретические отклонения еi нельзя рассчитать, их обычно заменяют на фактические отклонения зависимой переменной от линии регрессии ^., для которых формулируются те же исходные требования, что и для єi). В этом случае квадратную матрицу ковариаций cov(ei, ej) можно представить в виде:

где cov(ei, ej)=0 при i ¹ j; cov(ei, ej)=S2; п - длина рассматриваемого временного ряда.

Если величины 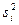известны, то далее можно применить взвешенный МНК, используя в качестве весов величины 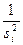и минимизируя сумму

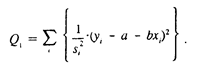
Формула Q, записана для парной регрессии; аналогичный вид она имеет и для множественной линейной регрессии. При использовании IVLS оценки параметров не только получаются несмещенными (они будут таковыми и для обычного МНК), но и более точными (имеют меньшую дисперсию), чем не взвешенные оценки.

Проблема заключается в том, чтобы оценить величины s2, поскольку заранее они обычно неизвестны. Поэтому, используя на первом этапе обычный МНК, нужно попробовать выяснить причину и характер различий дисперсий еi. Для экономических данных, например, величина средней ошибки может быть пропорциональна абсолютному значению независимой переменной. Это можно проверить статистически и включить в расчет МНК веса, равные .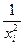

Существуют специальные критерии и процедуры проверки равенства дисперсий отклонений. Например, можно рассмотреть частное от деления cумм самых больших и самых маленьких квадратов отклонений, которое должно иметь распределение Фишера в случае гомоскедастичности.

Использование взвешенного метода в статистических пакетах, где предоставлена возможность задавать веса вручную, позволяет регулировать вклад тех или иных данных в результаты построения моделей. Это необходимо в тех случаях, когда мы априорно знаем о не типичности какой-то части информации, т.е. на зависимую переменную оказывали влияние факторы, заведомо не включаемые в модель. В качестве примера такой ситуации можно привести случаи стихийных бедствий, засух.