2015-05-18
6837
Многие экономические процессы наилучшим образом описываются нелинейными соотношениями, например, функциями спроса и производственными функциями. С этой целью в уравнение регрессии начали включаться переменные не только в первой, но и второй степени – с целью отразить свойства оптимальности экономических переменных, то есть наличия значений, при которых достигается минимальное или максимальное воздействие на зависимую переменную.
Предполагая, что ошибки измерения переменных сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели, то есть ошибкам, вызванным неверным видом уравнения регрессии.
В парной регрессии выбор вида математической функции, моделирующей связь переменных, может быть осуществлен тремя методами:
1) графическим;
2) аналитическим, то есть исходя из теории изучаемой взаимосвязи;
3) экспериментальным.
При изучении зависимости между двумя признаками наиболее наглядным является графический метод подбора уравнения. Он основан на построении поля корреляции. Основные типы кривых, используемых при количественной оценке связей, представлены на рисунке.
|
|
|
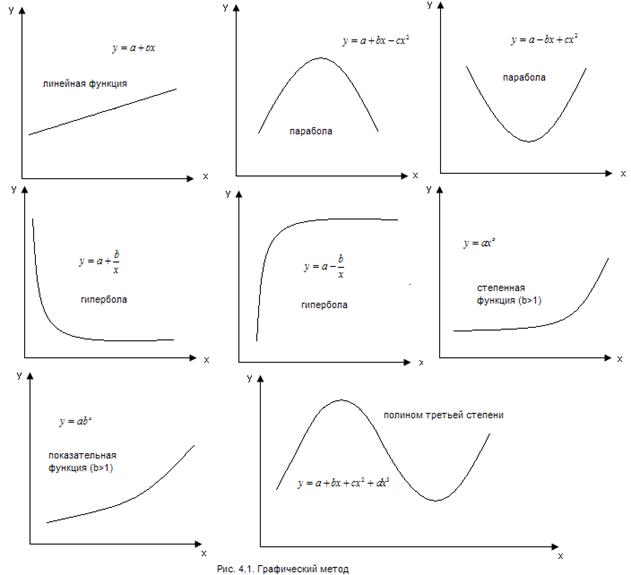
Значительный интерес представляет аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых переменных. Пусть, например, изучается потребность предприятия в электроэнергии у в зависимости от объема выпускаемой продукции х. Все потребление электроэнергии можно подразделить на две части:
1) не связанное с производством продукции (а);
2) непосредственно связанное с объемом выпускаемой продукции, пропорционально возрастающее с увеличением объема выпуска (в*х).
Тогда зависимость потребления электроэнергии от объема продукции можно выразить уравнением регрессии вида у = а + вх. Если затем разделить обе части уравнения на величину объема выпуска продукции (х), то получим выражение зависимости удельного расхода электроэнергии на единицу продукции z = у/х от объема выпущенной продукции (х) в виде уравнения равносторонней гиперболы z = в + а/х.
Аналогично, текущие производственные затраты предприятия могут быть подразделены на условно-постоянные и условно-переменные, и тогда зависимость себестоимости единицы продукции от объемов производства также характеризуется равносторонней гиперболой.
Выбор вида уравнения регрессии экспериментальным методом обычно осуществляется при обработке информации на компьютере путем сравнения величины остаточной дисперсии, рассчитанной при разных моделях. Чем меньше величина остаточной дисперсии, тем в меньшей мере наблюдается влияние прочих, не учитываемых в уравнении регрессии факторов, тем лучше уравнение регрессии подходит к исходным данным. Если остаточная дисперсия оказывается примерно одинаковой для нескольких функций, то на практике предпочтение отдается более простым видам функций, ибо они в лучшей степени поддаются интерпретации и требуют меньшего объема наблюдений. Число наблюдений должно в 6-7 раз превышать число рассчитываемых параметров при переменной х.
|
|
|
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. В общем случае линейное уравнение выглядит так, что каждый объясняющий элемент, за исключением постоянной величины, записан в виде произведения переменной и коэффициента
у = a + b1х1 + b2х2 +...
Уравнения вида у = a +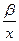 
и у = a х b являются нелинейными. Эти зависимости считаются приемлемыми для описания кривых Энгеля, характеризующих соотношение между спросом на определенный товар (у) и общей суммой дохода (х). Как можно определить параметры a и b в каждом уравнении, зная значения у и х? В конечном счете в обоих случаях можно применить линейный регрессионный анализ, для этого потребуется лишь небольшая подготовка.
Различают два класса нелинейных регрессий:
1) регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам. Примером этого класса моделей могут служить полиномы разных степеней у = а + вх + сх2; у = а + вх + сх2+ dх3, а также равносторонняя гипербола у = в + а/х.
2) нелинейные регрессии по оцениваемым параметрам:
- степенная у = а хв
- показательная у = а вх
- экспоненциальная у = е а+ вх.
Первый класс моделей (нелинейных по переменным) не таит каких-либо сложностей в оценке ее параметров. Она определяется, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в параболе у = а + вх + сх2, заменяя переменные х1=х, а х2=х2, получаем двухфакторное уравнение линейной регрессии у = а + вх1 + сх2. Соответственно для полинома третьего порядка получим трехфакторную модель линейной регрессии и так далее.Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров. Среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени, в отдельных случаях – полином третьего порядка. Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и, соответственно, тем менее однородна совокупность по результативному признаку.
Для равносторонней гиперболы мы можем заменить 1/х на z и получим линейное уравнение регрессии, оценка параметров которого может быть дана МНК.
Иначе обстоит дело со вторым классом моделей, то есть с регрессией, нелинейной по оцениваемым параметрам. Данный класс нелинейных моделей можно разделить на два типа: а) нелинейные модели внутренне линейные и б) нелинейные модели внутренне нелинейные.
Если модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Пример – степенная функция у = а хв. Данная модель нелинейна относительно оцениваемых параметров, так как включает параметры а и в неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения приводит его к линейному виду. Соответственно оценки параметров а и в могут быть найдены МНК.
Внутренне нелинейной будет модель вида у = а + вхс, так как ее невозможно превратить в линейный вид никакими преобразованиями переменных.
Коэффициенты эластичности в нелинейных регрессиях:
|
|
|
Степенная функция используется в эконометрических исследованиях очень широко. Связано это с тем, что параметр b в ней имеет четкое экономическое истолкование, то есть он является коэффициентом эластичности. Это значит, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.
О правомерности подобного истолкования параметра b можно судить, если рассмотреть формулу расчета коэффициента эластичности
Э=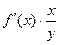 
, где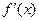 
- первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи. Для степенной функции она составит 
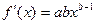. Соответственно коэффициент эластичности окажется равным
Э =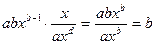 
Коэффициент эластичности можно определить и для других форм связи, но только для степенной функции он представляет собой постоянную величину, равную параметру b. В других функциях коэффициент эластичности зависит от значения фактора х. Так, для линейной регрессии у=а+bх коэффициент эластичности определяется по формуле
Э=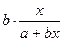 
, так как 
.
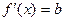В силу того, что для линейной функции коэффициент эластичности не является величиной постоянной, а зависит от соответствующего значения х, то обычно рассчитывается средний показатель эластичности по формуле
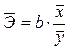
Для параболы второго порядка у=а+bx+cx2 первая производная функции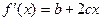 
, а коэффициент эластичности также зависит от величины х
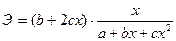
Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчет экономического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в %. Например, не имеет смысла определять в % такие признаки, как возраст, число комнат, тарифный разряд рабочего и др. В такой ситуации степенная функция не может быть экономически интерпретирована, поэтому даже если она оказывается наилучшей по формальным математическим соображениям (минимальная остаточная дисперсия), значительно больший интерес для интерпретации может иметь линейная регрессия с меньшим коэффициентом корреляции.
|
|
|
Корреляция для нелинейной регрессии:
Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем тесноты связи, а именно – индексом корреляции R
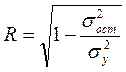
где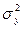 
-общая дисперсия результативного признака;
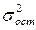- остаточная дисперсия.
Учитывая связь дисперсии с объемом вариации, можно легко доказать, что индекс корреляции через объемы вариации определяется следующим образом:
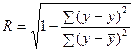
Величина данного показателя находится в пределах от нуля до единицы. Чем он ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.
Парабола второй степени, как и полином более высокого порядка, при линеаризации принимает вид уравнения множественной регрессии. Если же нелинейное относительно объясняющей переменной уравнение регрессии при линеаризации принимает форму линейного уравнения парной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции, величина которого совпадет с индексом корреляции.
Обратимся к равносторонней гиперболе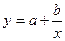 
. Заменив 
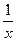на z, имеем регрессию вида 
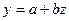, для которой может быть определен линейный коэффициент корреляции 
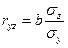. По своей величине он будет равен коэффициенту корреляции между у и х, то есть ryч.
Квадрат индекса корреляции (i2) называют индекс детерминации, он имеет тот же смысл, что и линейный коэффициент детерминации, то есть представляет собой отношение факторной и общей суммы квадратов отклонений.
Индекс детерминации используется для проверки существенности уравнения нелинейной регрессии в целом по F-критерию Фишера
F =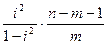 
где п – число наблюдений;
т – число параметров при переменных х.
Величина m характеризует число степеней свободы для факторной дисперсии, а (n – m – 1) – число степеней свободы для остаточной суммы квадратов. Для степенной функции т =1 и формула F-критерия примет тот же вид, что и при линейной парной зависимости
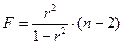
Индекс детерминации можно сравнивать с коэффициентом детерминации для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем меньше значение линейного коэффициента детерминации по сравнению с индексом детерминации. Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически если величина i2-r2≤0.1, то предположение о линейной форме связи считается оправданным. Иными словами, если нет уверенности в правильности выбора нелинейной функции, то в целях лучшей интерпретации связи она может быть заменена уравнением прямой.
Если, например, изучается зависимость объема продукции предприятия от занимаемых площадей, числа работников, стоимости основных фондов (или всего капитала), то каждый из факторов является необходимым для существования результата, а не добавлением к нему. В таких ситуациях нужно исходить из гипотезы о мультипликативной форме модели:
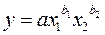
Такая модель по ее первым создателям получила название модель Кобба-Дугласа. Это степенная функция и, как мы уже знаем, показатели степени при факторах являются коэффициентами эластичности. Они показывают, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1 процент при неизменности других факторов. Решение степенной функции методом наименьших квадратов требует предварительной ее линеаризации. Как было рассмотрено ранее, линеаризация степенных функций проводится с помощью логарифмирования ее переменных.
Степенные множественные функции часто используются как производственные функции, где результатом выступают объемы производства, а факторами – используемые ресурсы (трудовые ресурсы, основные производственные фонды, машины, текущие затраты и т.п.). Экономический смысл здесь имеют не только коэффициенты эластичности по каждому фактору, но и их сумма
B = b1+b2
Эта величина фиксирует обобщенную характеристику эластичности производства (показывает, на сколько процентов в среднем увеличиваются объемы производства при увеличении всех факторов на 1%).
Возможны и другие линеаризуемые функции для построения уравнения множественной регрессии. Например,
экспонента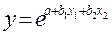 
или гипербола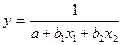 
!!! Дополнительно: отдельные виды не линейных функций
Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную, или обратная на прямую. В этом случае определяется значение фактора, при котором достигается минимальное или максимальное значение результативного признака. Для этого приравнивают к нулю первую производную параболы второй степени
у = а +вх+сх2,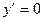 
, то есть в+2сх=0 и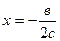 
Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболы второго порядка становятся трудно интерпретируемыми, и поэтому форму связи можно заменить другими нелинейными моделями.
Если в>0 и с<0, то кривая симметрична относительно высшей точки, то есть точки перелома кривой, изменяющей рост на падение. В анализе таких функций часто определяется значение фактора, при котором достигается максимум результата. Например, предполагая, что зависимость урожайности от дозы внесения удобрений характеризуется уравнением вида у = 5 + 1,5х – 0,1х2, мы найдем величину дозы удобрений, обеспечивающую максимальную урожайность. Приравнивая к нулю первую производную, имеем 1,5 – 2*0,1х = 0
Максимальная урожайность достигается при дозе удобрений х = 1,5/0,2 = 7,5.
При в<0 и с>0 парабола второго порядка симметрична относительно своей низшей точки. Это позволяет определить минимум функции в точке, меняющей направление связи, то есть снижение на рост (например, найти выпуск продукции, при котором достигаются минимальные удельные затраты). Чаще всего исследователь имеет дело лишь с отдельными сегментами параболы, а не с полной симметричной параболической формой. Поэтому если график зависимости не демонстрирует четко выраженной смены направленности связи признаков, то она может быть выражена другой нелинейной функцией (например, степенной).
