Парная регрессия характеризует связь между двумя признаками: результативным (у) и факторным (х).
Оценка параметров уравнения регрессии осуществляется методом наименьших квадратов
Параметры уравнения прямой определяются путем решения системы нормальных уравнений
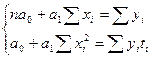 (1)
(1)
или по формулам:
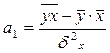 ; (2)
; (2)
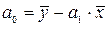 (3)
(3)
В уравнении прямой параметр а0 экономического смысла не имеет. Параметр а1 является коэффициентом регрессии и показывает изменение результативного признака при изменении факторного на единицу своего измерения. Теоретические значения результативного признака рассчитываются путем подстановки в уравнение регрессии значений факторного признака. При правильном расчете параметров уравнения регрессии сумма фактически значений результативного показателя должна быть равна сумме теоретических.
Оценка тесноты связи между признаками осуществляется с помощью коэффициента линейной парной корреляции - rx,y. Он может быть рассчитан по формуле: 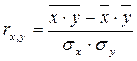 . Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии:
. Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии: 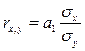 .
.
Область допустимых значений линейного коэффициента парной корреляции от –1 до +1. Знак коэффициента корреляции указывает направление связи. Если rx,y>0, то связь прямая; если rx,y<0, то связь обратная.
Если данный коэффициент по модулю близок к единице, то связь между признаками может быть интерпретирована как довольно тесная линейная. Если его модуль равен единице êrx,y ê=1, то связь между признаками функциональная линейная. Если признаки х и y линейно независимы, то rx,y близок к 0.
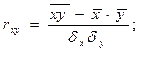 (4)
(4)
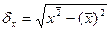 (5)
(5)
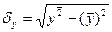 (6)
(6)
Коэффициент детерминации – коэффициент корреляции, возведенный в квадрат. Он показывает долю вариации результативного признака, обусловленную вариацией факторного признака.
Для оценки статистической значимости коэффициента регрессии и корреляции рассчитывается t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается нулевая гипотеза о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки.

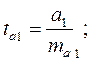 (7)
(7)
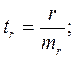 (8)
(8)
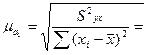
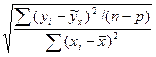 (9)
(9)
где n- численность выборки;
p- число параметров в уравнении регрессии
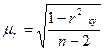 (10)
(10)
Сравнивая фактическое и критическое (табличное) значения t - статистики, принимаем или отвергаем сформулированную нулевую гипотезу. Если фактическое значение коэффициента Стьюдента больше табличного значения, то нулевая гипотеза отклоняется, то есть параметры a1, и r не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если табличное значение коэффициента Стьюдента больше фактического, то нулевая гипотеза не отклоняется и признается случайная природа формирования параметров модели и коэффициента корреляции.
Среднюю ошибку и коэффициент Стьюдента для коэффициента корреляции вычисляем по формулам (7.9, 7.10).
Для расчета доверительного интервала определяется предельная ошибка для каждого показателя:
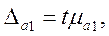 (11)
(11)
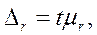 (12)
(12)
где t – значение нормированного отклонения, величина которого определяется по таблицам.
Доверительные границы коэффициентов регрессии и коэффициента корреляции в генеральной совокупности составят
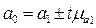 (13)
(13)
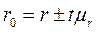 (14)
(14)
Если в границы доверительного интервала попадает ноль и нижняя граница отрицательная, а верхняя положительна, то оцениваемый параметр принимается равным нулю, так как он не может одновременно принимать и положительное и отрицательное значение.
Прогнозируемое значение результативного показателя определяется путем подстановки в уравнение регрессии соответствующего прогнозируемого значения факторного признака – х. Затем вычисляется средняя ошибка прогноза по формуле:
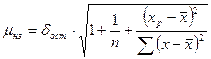 , (15)
, (15)
где 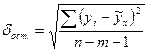 (16)
(16)
Доверительный интервал прогноза строится на основании предельной ошибки прогноза, которая рассчитывается путем умножения средней ошибки на коэффициент Стьюдента с вероятностью нулевой гипотезы 0,05 и числом степеней свободы n-m-1.
 2015-05-18
2015-05-18 710
710








