Натуральная и стандартизованная формы модели множественной регрессии

Параметры уравнения множественной линейной регрессии определяются, как и в парной регрессии, с помощью метода наименьших квадратов. При его применении должна минимизироваться остаточная сумма квадратов отклонений фактических величин от теоретических. Для уравнения множественной регрессии 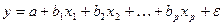это выглядит следующим образом:

.

В данном случае неизвестными являются параметры уравнения регрессии а, b₁, b₂, …,b_p. Чтобы их найти, дифференцируют сумму S по этим переменным и приравнивают производные к нулю. В итоге получается система уравнений, решение которой и позволяет определить параметры а, b₁, b₂, …,b_p. Т.е., так же, как и в модели парной линейной регрессии.

Уравнение множественной линейной регрессии, построенное по исходным данным, называется моделью в натуральной форме или в натуральном масштабе. Если провести стандартизацию переменных, входящих в модель, т.е. выполнить следующие преобразования:

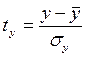; для всех i, а затем построить по новым данным модель множественной регрессии 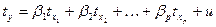, то такая модель будет называться моделью в стандартизированной форме или стандартизированном масштабе. Стандартизированные переменные имеют среднее, равное нулю, и среднее квадратическое отклонение, равное единице. Коэффициенты модели в стандартизированной форме отличаются от коэффициентов исходной модели и поэтому обозначены другими символами - 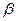, а случайный остаток – u. Свободный член в этой модели отсутствует, что следует из свойств стандартизированной переменной.

Определить 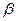-коэффициенты можно с помощью МНК. Применяя его к уравнению множественной регрессии в стандартизированном масштабе, после соответствующих преобразований получаем систему нормальных уравнений следующего вида:

Решая ее методом определителей, находим 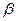-коэффициенты.

Решать такую систему удобно методом определителей.

,

где 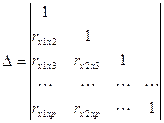- главный определитель системы.

Второстепенные определители получаются путем замены соответствующего столбца матрицы столбцом свободных членов.

С уравнением регрессии в стандартизированном масштабе работать удобно, поскольку парные линейные коэффициенты корреляции r рассчитываются еще на этапе отбора факторов.

От 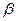-коэффициентов можно перейти к обычным параметрам b₁, b₂, …,b_p с помощью формулы:

.

Параметр а определяется следующим образом:

.

Существует другой способ нахождения параметров уравнения линейной множественной регрессии.

Совокупность значений независимых переменных представляют в виде матрицы:

,

где n – количество наблюдений,

m – количество факторов (независимых переменных).

Совокупность значений зависимой переменной представляют в виде матрицы-столбца:

.

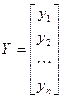Тогда значения параметров уравнения линейной множественной регрессии будут находиться в ячейках матрицы В:

.

Матрица-столбец В определяется по формуле:

,

где X^T – транспонированная матрица, находится с помощью функции Excel ТРАНСП;

(X^TX) – произведение соответствующих матриц, определяется с помощью функции Excel МУМНОЖ;

(X^TX)^-1 – обратная матрица, вычисляется с помощью функции Excel МОБР;

X^TY – произведение матриц, вычисляется с помощью функции Excel МУМНОЖ;

(X^TX)^-1 X^TY – искомая матрица столбец, вычисляемая как произведение найденных матриц (X^TX)^-1 и X^TY.