2015-05-18
832
Проверим выполнение условия 1: математическое ожидание случайной переменной равно нулю, т. е. М (e) = 0.
Оценкой математического ожидания случайной переменной М (e) является среднее остатков 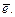 Гипотеза о значимости математического ожидания случайной переменной проверяется с помощью t- статистики, наблюдаемое значение которой определяется равенством 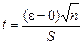 . По распреде- лению Стьюдента по заданному уровню значимости a и числу степеней свободы v = n – 1 находится критическая точка 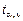 = tкр. Если tнабл > tкр, то М (e) значимо. Если tнабл < tкр, то М (e) незначимо.
Если условие 1 нарушено, то оценки коэффициентов регрессии могут быть смещенными. Поэтому для устранения этих проблем в модель регрессии следует включать свободный член.
|
Среднее остатков рассчитано на листе «Условие 1 и нормальность»в таблице «Остатки» (таблица 9).
Среднее равно –1,7E–14 = –1,7∙10–14. Оно достаточно близко к нулю, поэтому можно предположить, что математическое ожидание случайной переменной равно нулю, т. е. выполняется условие 1. Проверим гипотезу о равенстве нулю математического ожидания случайной переменной.
|
|
|
Таблица 9 – Числовые характеристики остатков
| Остатки | |
| Среднее | –1,7E–14 |
| Стандартная ошибка | 3,02 |
| Медиана | –1,46 |
| Мода | #Н/Д |
| Стандартное отклонение | 13,67 |
| Дисперсия выборки | 186,74 |
| Эксцесс | 0,08 |
| Асимметричность | –0,3 |
| Интервал | 55,91 |
| Минимум | –29,4 |
| Максимум | 26,51 |
| Сумма | –3,4E–13 |
| Счет | |
| Уровень надежности (95%) | 6,4 |
На листе «Условие 1 и нормальность» рассчитаны наблюдаемое и критическое значения статистики (таблица 10).
Таблица 10 – Значимость математического ожидания случайного члена
| tнабл | –5,58E–15 |
| tкр | 2,09 |
Так как |tнабл| = 5,58E–15 = 5,58∙10-15 < tкр = 2,09, то среднее не значимо (незначительно отличается от нуля). Следовательно, условие 1 Гаусса–Маркова выполняется.
