Нелинейная регрессия. Нелинейные модели и их линеаризация

Нелинейная регрессия — частный случай регрессионного анализа, в котором рассматриваемая регрессионная модель есть функция, зависящая от параметров и от одной или нескольких свободных переменных. Зависимость от параметров предполагается нелинейной.

Многие экономические зависимости не являются линейными по своей сути, и

поэтому их моделирование возможно лишь на основе нелинейных уравнений

регрессии. Различают два вида нелинейных моделей: нелинейные модели по

переменным и нелинейные модели по параметрам. Основные типы нелинейных моделей:

1) Обобщенная модель нелинейная по переменным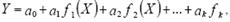

2)Степенные функции 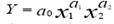, 3) Показательные функциb 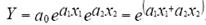, 4) Показательно-степенные функции 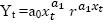. Основной прием, который используется для построения нелинейных регрессионных моделей – линеаризация, который заключается в искусственном

преобразовании исходной спецификации модели к линейному виду. Линеаризация

обобщенной нелинейной модели: 1. Вводятся новые переменные: 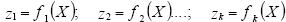Подставляя новые переменные в модель (1),

получим модель линейную по переменным z: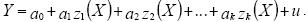

Линеаризация степенной модели, нелинейной по параметрам: 1. Метод линеаризации

– логарифмирование с последующим введением новых переменных: 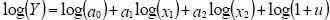2. Вводятся новые переменные и

параметры: 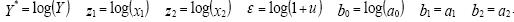. В

новых переменных исходное уравнение принимает вид уравнения множественной 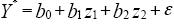. 3. Оцениваются параметры b0, b1, b2 – методом

наименьших квадратов и проверяются гипотезы о выполнении предпосылок теоремы

Гаусса-Маркова для модели. 4. Осуществляется возврат к исходной модели 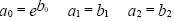. Линеаризация показательной (экспоненциальной) модели:

1. Метод линеаризации – логарифмирование 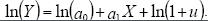.2. Введение

новых переменных и параметров: 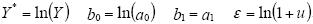. 3. Оценка

линейной регрессионной модели 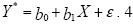. 4. Обратный переход к исходной

модели. Линеаризация показательно-степенной модели: производится так же с

помощью логарифмирования и последующей замены переменных.