Решение. а) Произведем отбор информативных факторов во множественную модель

а) Произведем отбор информативных факторов во множественную модель:

Парный коэффициент корреляции 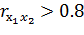, 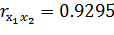. Исходя из этого, можно предполагать наличие мультиколлинерности по признаку мультиколлинерности.

1.

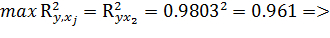
для y наиболее информативным является переменная x₂, вклычаем в модель х₂.

2.

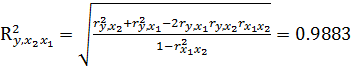
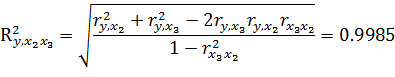
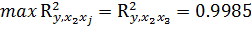
Вычислим скорректированный коэффициент корреляции:

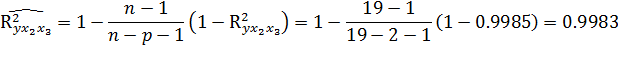
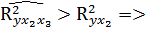вклычаем в модель х₃.

3.

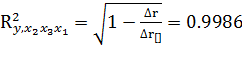
Вычислим скорректированный коэффициент корреляции:

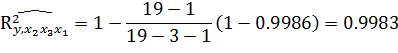
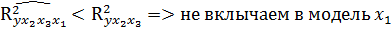
б) Уравнение множественной регрессии в стандартизованном масштабе имеет вид:

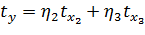
Коэффициенты 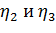находим из системы:

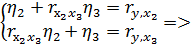
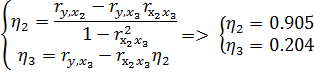
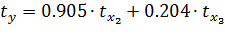
Подсчитаем коэффициенты эластичности:

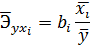
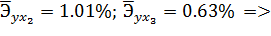
х₂ оказывает на у большее влияние.

в) Рассчитаем параметры уравнения в естественной форме:

.

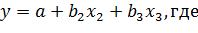
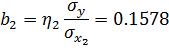
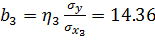
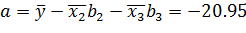Уравнение в естественной форме:

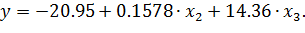
По критерию Фишера определим, значимо ли уравнение:

.

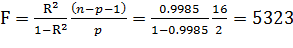
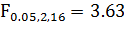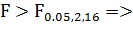уравнение значимо.

г) Рассчитаем прогнозное значение результата, предполагая, что прогнозные значения факторов составят 104 % от их среднего значения:

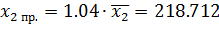
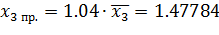
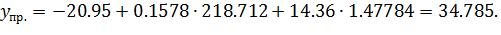(млрд. руб.)