Решение

№	x	у	х2	у2	ху
	103.6	69.0	10732.96	4761.00	7148.40
	102.2	69.8	10444.84	4872.04	7133.56
	100.1	70.6	10020.01	4984.36	7067.06
	97.8	71.4	9564.84	5097.96	6982.92
	95.9	72.4	9196.81	5241.76	6943.16
	96.4	70.2	9292.96	4928.04	6767.28
	97.3	71.1	9467.29	5055.21	6918.03
средн.	99.04	70.64	9817.10	4991.48	6994.34
𝜎2	8.18	1.47
𝜎	2.86	1.21

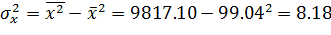
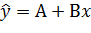
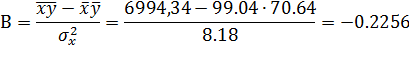
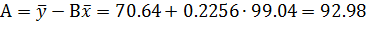
Получаем уравнение регрессии:

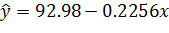
Проверьте значимость регрессии:

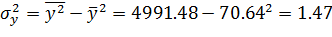
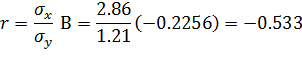
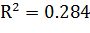
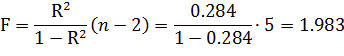
При уровне значимости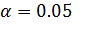

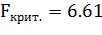
При уровне значимости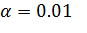

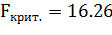
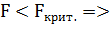уравнение незначимо.

Найдем стандартные ошибки коэффициентов и проверим значимость коэффициентов уравнения регрессии:

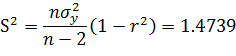
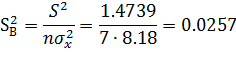
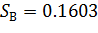
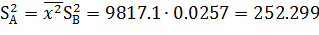
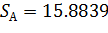
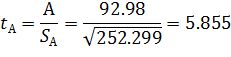
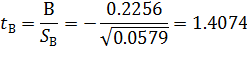
При доверительной вероятности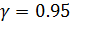

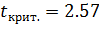
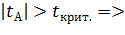коэффициент А значим

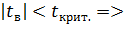коэффициент В незначим

Проверим гипотезу

Н₀: рост доходов на 1 млрд. вызывает увеличение потребления на 1 млрд.

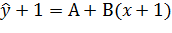
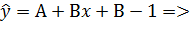
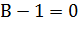
Н₀: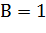

Но по подсчетам 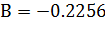. Таким образом гипотеза Н₀ не верна:

рост доходов на 1 млрд. не вызывает увеличение потребления на 1 млрд.

Задача 3.

Две студентки 2 курса экономического факультета вычисляют одну и ту же величину А. Из-за неточности вычислений они получают два различных ответа: 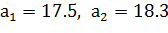Будем условно считать, что 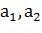– независимые случайные величины с математическим ожиданием 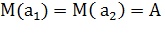. Первая студентка утверждает, что допускает при вычислениях дисперсию 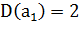, а вторая-

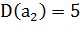. Сделайте на основе этих данных наилучшую линейную оценку величины А.