Металлы

Рис. 33.5

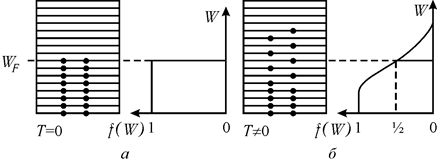
На рис. 33.5, а схематически показано заполнение электронами зоны проводимости для щелочного металла (лития) при T = 0. Видно, что в этом случае электроны заполняют все нижние подуровни энергии вплоть до некоторого уровня WF, называемого уровнем Ферми. При T > 0 часть электронов может переходить на более высокие уровни (рис. 33.5, б).

В частично заполненной зоне проводимости металла электроны могут переходить на более высокие уровни энергии не только за счет теплового движения, но и под воздействием внешнего электрического поля, которое приводит электроны в упорядоченное движение. Эти переходы возможны, так как подуровни энергии в зоне расположены очень близко друг к другу и не заполнены электронами. В связи с этим металлы являются хорошими проводниками.

Рассмотрим теперь вопрос о теплоемкости металлов. Согласно классической теории атомная теплоемкость металлов должна быть выше, чем у диэлектриков, поскольку находящиеся в металле свободные электроны (электронный газ) должны обладать дополнительной теплоемкостью. Однако экспериментально показано, что атомная теплоемкость металла равна атомной теплоемкости диэлектриков. Для выяснения причин такого расхождения изложим классическую и квантовую теории теплоемкости электронного газа.

В соответствии с классическими представлениями средняя кинетическая энергия движения электронов должна быть равна ³/₂kT, поэтому внутренняя энергия электронов, находящихся в 1 кг-атоме металла,

,

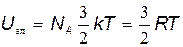где NA — число Авогадро. Теплоемкость электронного газа

,

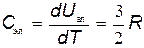в то время как эксперимент показывает, что Cэл=0

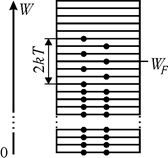Рис. 33.6

Причина такого расхождения заключается в том, что в тепловое движение вовлекаются не все электроны, а только та их часть, энергия которых отличается от энергии Ферми на величину ±kT. Эти электроны заполняют энергетический интервал шириной 2kT: от WF –kT до WF +kT (рис. 33.6). Электроны, заполняющие нижние подуровни энергии, не могут увеличить свою энергию, поскольку более высокие подуровни энергии заняты, а переход туда еще одного электрона запрещен принципом Паули. Такие электроны в тепловом движении не участвуют.

Пусть N — число электронов, находящихся в энергетическом интервале шириной 2kT вблизи уровня Ферми, а NA — общее число свободных электронов в 1 кг-атоме металла (при T=0 эти электроны заполняют энергетический интервал от 0 до WF). Решая пропорцию

N — 2kT;

NA — WF,

находим число электронов, принимающих участие в тепловом движении:

.

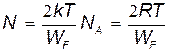Внутреннюю энергию этой части электронного газа найдем, умножив N на среднюю энергию теплового движения электрона:

.

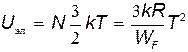Тогда теплоемкость электронного газа

.

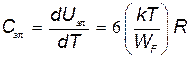(33.3)

Как показывают расчеты, энергия Ферми для металлов WF ~ 10 эВ. Этой энергии соответствует так называемая температура Ферми TF = WF/k~10⁵ К.

Если преобразовать (33.3) к виду

,

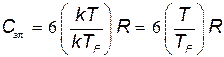то с учетом того, что T/TF << 1 для любых температур ниже температуры плавления металла, приходим к выводу, что в полном согласии с экспериментом Cэл = 0.

В заключение рассмотрим современную квантово-механическую трактовку зависимости сопротивления металла от температуры. Как и в классической теории электропроводности, при квантово-механическом рассмотрении движения электронов в металле оказывается справедливым выражение (15.29) для удельного сопротивления r.

В рамках классической теории теплопроводности предполагалось, что 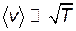и, следовательно, удельное сопротивление 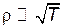, что противоречит эксперименту, где наблюдается линейная зависимость сопротивления металлов от температуры.

В квантовой теории металлов энергия электронов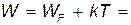
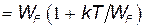Поскольку 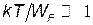, то энергия электронов и, следовательно, скорость их теплового движения практически не зависит от температуры. Зависимость же удельного сопротивления металлов от температуры объясняется уменьшением средней длины свободного пробега электронов от температуры (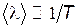), что связано с более эффективным рассеянием электронов на тепловых колебаниях ионов кристаллической решетке при более высоких температурах.