Соленоидальное векторное поле

18.2.1. Определение соленоидального поля. Векторное поле 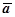(M) называется соленоидальным в области V, если во всех точках этой области .

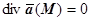Согласно этому определению, поле не может иметь в области V источников и стоков; таким свойством обладает магнитное поле соленоида, что и объясняет происхождение термина.

Соленоидально поле ротора любого достаточно гладкого поля: .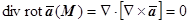

Самостоятельно доказать это свойство в координатной форме.

18.2.2. Свойства соленоидального поля.

1. Поток соленоидального векторного поля через поверхность 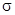, ограничивающую область 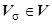, равен нулю. Это прямое следствие формулы Остроградского.

2. Верно и обратное утверждение: равенство нулю потока через любую замкнутую поверхность 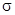достаточно для соленоидальности поля 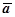(M). Действительно, в разделе 17.3.5. Инвариантное определение дивергенции мы доказали, что 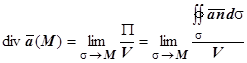, и,так как 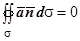, то .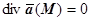

3. Пусть в V имеется изолированный источник (или сток) поля. Если поле 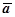(M) соленоидально, то его поток через любую замкнутую поверхность 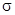, содержащую этот источник, имеет одно и то же значение.

Фраза " в V имеется изолированный источник (или сток) поля" означает, что область V, в которой поле соленоидально, неодносвязна; из V выколота точка, в которой находится источник. Так, поле электрической напряжённости, создаваемое зарядом q, 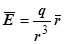, соленоидально всюду, кроме точки 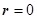, в которой расположен источник.

4. Поток соленоидального векторного поля через любое поперечное сечение векторной трубки один и тот же. Это следует из того, что поток через боковую поверхность трубки равен нулю.