Теорема. Если область V и поле 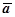 (M) удовлетворяют следующим условиям:
(M) удовлетворяют следующим условиям:
1. V - односвязная область;
2. Поле 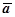 (M) - безвихрево (т.е.
(M) - безвихрево (т.е. 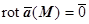 ),,
),,
то 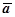 (M) - потенциальное в V поле.
(M) - потенциальное в V поле.
 Доказательство. Напомним определение односвязной области: область (на плоскости, в пространстве) называется односвязной, если любой замкнутый контур, лежащий в этой области, можно непрерывной деформацией стянуть в точку, не выходя при этом за пределы области. Нам при доказательстве теоремы придётся строить поверхности, натянутые на контуры; определение односвязности как раз гарантирует, что такие поверхности существуют, и ими могут служить поверхности, образующиеся при деформации контура в точку.
Доказательство. Напомним определение односвязной области: область (на плоскости, в пространстве) называется односвязной, если любой замкнутый контур, лежащий в этой области, можно непрерывной деформацией стянуть в точку, не выходя при этом за пределы области. Нам при доказательстве теоремы придётся строить поверхности, натянутые на контуры; определение односвязности как раз гарантирует, что такие поверхности существуют, и ими могут служить поверхности, образующиеся при деформации контура в точку.
1. Докажем, что если выполняются условия теоремы, то линейный интеграл поля 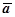 (M) по любой кривой
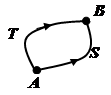
(M) по любой кривой 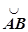 , целиком лежащей в V, определяется только начальной и конечной точками этой кривой, и не зависит от её формы. Пусть ASB и ATB - два пути, соединяющие точки А и В. Вместе они образуют замкнутый контур ASBTA. Пусть
, целиком лежащей в V, определяется только начальной и конечной точками этой кривой, и не зависит от её формы. Пусть ASB и ATB - два пути, соединяющие точки А и В. Вместе они образуют замкнутый контур ASBTA. Пусть 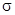 - кусочно-гладкая поверхность, натянутая на этот контур. Тогда по формуле Стокса
- кусочно-гладкая поверхность, натянутая на этот контур. Тогда по формуле Стокса 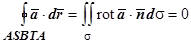 , так как
, так как 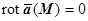 . Но
. Но 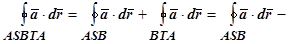
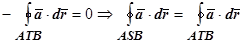 .
.
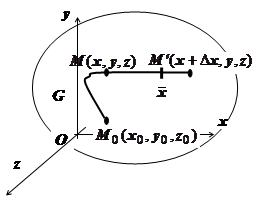 2. Докажем, что если мы фиксируем точку
2. Докажем, что если мы фиксируем точку 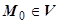 и возьмём
и возьмём 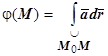 , то
, то 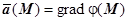 , т.е. определённая таким образом функция
, т.е. определённая таким образом функция 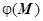 действительно является потенциалом поля
действительно является потенциалом поля 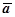 (M). Это доказательство полностью повторяет доказательство теоремы пункта 16.3.3.6. Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути. Именно, требуется доказать, что
(M). Это доказательство полностью повторяет доказательство теоремы пункта 16.3.3.6. Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути. Именно, требуется доказать, что 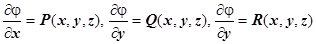 . Действительно, пусть
. Действительно, пусть 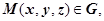
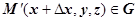 . Тогда
. Тогда 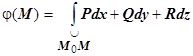 ,
,
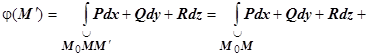
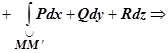
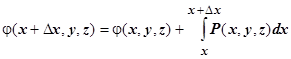 (на
(на 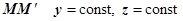 )
) 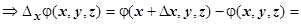
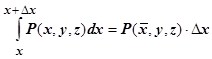 (по теореме о среднем)
(по теореме о среднем) 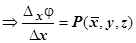 . Точка
. Точка 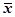 удовлетворяет условиям
удовлетворяет условиям 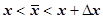 . Устремим
. Устремим 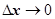 , тогда
, тогда 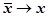 , и
, и 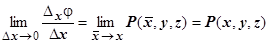 .
.
Аналогично доказывается, что 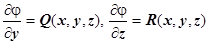 .
.
 18.1.4. Нахождение потенциала. В предыдущем разделе мы доказали, что если выполняются условия потенциальности поля
18.1.4. Нахождение потенциала. В предыдущем разделе мы доказали, что если выполняются условия потенциальности поля 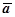 (M), то
(M), то 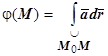 , где
, где 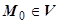 - фиксированная точка. Обычно, если в точке О (0,0,0) поле не имеет особенностей, то в качестве точки
- фиксированная точка. Обычно, если в точке О (0,0,0) поле не имеет особенностей, то в качестве точки 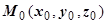 берётся именно эта точка; если в этой точке поле не определено, берётся другая точка. Интегрирование ведут по пути, состоящим из отрезков, параллельных координатным осям. В результате получим
берётся именно эта точка; если в этой точке поле не определено, берётся другая точка. Интегрирование ведут по пути, состоящим из отрезков, параллельных координатным осям. В результате получим 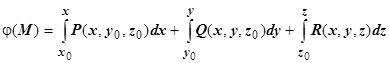 .
.
Пример. Доказать, что поле 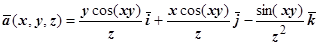 потенциально, и найти потенциал этого поля.
потенциально, и найти потенциал этого поля.
Решение. Мы будем доказывать, что это поле потенциально в любой односвязной области V, не содержащей точку О (0,0,0). Условие безвихревости поля 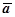 :
:
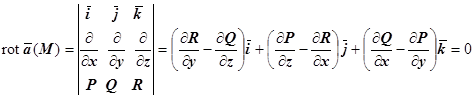 в координатной форме сводится к равенствам
в координатной форме сводится к равенствам  ,
, 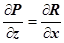 ,
, 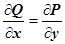 . В нашем поле
. В нашем поле 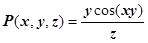 ,
, 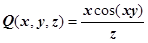 ,
, 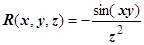 . Находим производные:
. Находим производные:
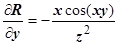 ,
, 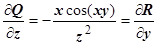 ;
; 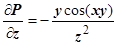 ,
, 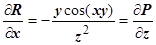 ;
; 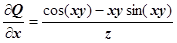 ,
, 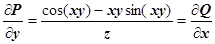 . Потенциальность поля доказана.
. Потенциальность поля доказана.
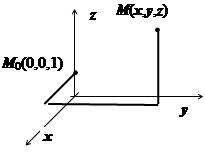
Ищем потенциал. Интеграл 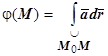 вычисляем по изображённому на рисунке пути, отправляясь от точки М 0(0,0,1).
вычисляем по изображённому на рисунке пути, отправляясь от точки М 0(0,0,1). 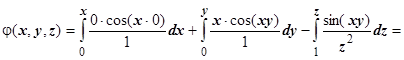
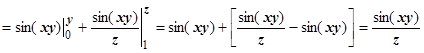 . Если бы мы взяли в качестве точки М 0 другую точку М 1, то получили бы выражение, отличающееся на некоторую постоянную (более точно, на
. Если бы мы взяли в качестве точки М 0 другую точку М 1, то получили бы выражение, отличающееся на некоторую постоянную (более точно, на 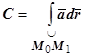 ); поэтому
); поэтому 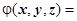
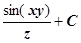 .
.
 2015-05-18
2015-05-18 2109
2109
