Гармонические поля

18.3.1. Оператор Лапласа. Пусть функция 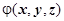имеет непрерывные вторые частные производные. Вычислим 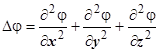. Оператор 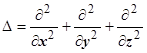, с помощью которого по функции 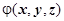получена функция 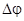, называется оператором Лапласа, или лапласианом. Формально его можно получить возведением в скалярный квадрат оператора Гамильтона набла:

.

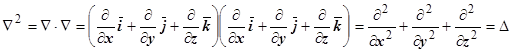Можно дать другое представление оператора Лапласа: 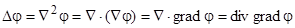, и это будет уже инвариантным определением оператора.

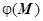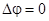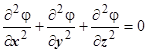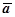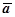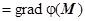18.3.2. Гармонические поля. Скалярное поле называется гармоническим, если оно удовлетворяет уравнению Лапласа , или . Векторное поле (M) называется гармоническим, если оно является градиентом некоторой гармонической функции, т.е. (M) , где .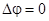

Из этого определения следует, что гармоническое векторное поле одновременно потенциально и соленоидально, так как 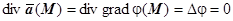. Верно и обратное: если 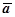(M) одновременно и потенциально, и соленоидально, то оно является гармоническим. Действительно, из потенциальности 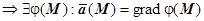, из соленоидальности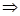 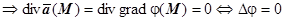, т.е. 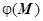- гармонический потенциал. Каждая координата гармонического векторного поля является гармонической функцией.