При рассмотрении геометрического метода решения задачи линейного программирования ограничимся рассмотрением совместной системы линейных неравенств с двумя и тремя переменными. Пусть, кроме того, задана линейная функция L = c1x1 + c2x2 + c0. Найдем среди множества точек (x1, x2) из области решений совместной системы неравенств такие, которые придают линейной функции L = c1x1 + c2x2 + c0 наименьшее (наибольшее) значение. Для каждой точки плоскости функция L принимает фиксированное значение L = L1. Множество таких точек есть прямая c1x1 + c2x2 + c0 = L1, расположенная нормально к вектору С(с1,с2), выходящему из начала координат. Если эту прямую передвигать параллельно самой себе в положительном направлении вектора С, то линейная функция L = c1x1 + c2x2 + c0 будет возрастать, а в обратном направлении – убывать. Пусть при движении прямой L в положительном направлении вектора С она впервые встретится с многоугольником решений в его вершине, тогда в этом положении L1 прямая L становится так называемой опорной, и на этой прямой функция L принимает наименьшее значение. При дальнейшем движении в том же направлении (положительном) прямая L пройдет через другую вершину многоугольника решений, выходя из области решений, и станет так же опорной прямой L2; ней функцияна L принимает наибольшее значение среди всех значений L, принимаемых на многоугольнике решений.
Таким образом, минимизация и максимизация линейной функции L = c1x1 + c2x2 + c0 на многоугольнике решений достигаются в точках пересечения этого многоугольника с опорными прямыми L = c1x1 + c2x2 + c0, нормальными к вектору С(с1,с2). Это пересечение опорной прямой может быть в одной точке (вершине многоугольника) или в бесконечном множестве точек (это множество есть сторона многоугольника).
Аналогично, линейная функция L = c1x1 +c2x2 +c3x3 +c0 Принимает постоянное значение на плоскости, нормальной к вектору С(с1,с2,с3). Наименьшее и наибольшее значения этой функции на многограннике решений достигается в точках пересечения этого многогранника с опорными плоскостями, нормальными к вектору С(с1,с2,с3). Пересечение многогранника с опорной плоскостью может происходить или в одной точке (вершине многогранника), или в бесконечном множестве точек (ребро или грань многогранника).
§ Пример
Максимизировать линейную форму L = 2x1 +2x2 при ограничениях:
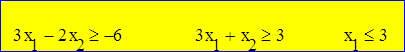
Решение.
Заменив знаки неравенств знаками точных равенств, построим область решений по уравнениям прямых: 3x1 -2x2 + 6 = 0, 3x1 +x2 – 3 = 0, x1 = 3.
Область решения – треугольник.
Построим вектор С (2,2). Тогда опорная прямая будет при выходе из треугольника решений проходить через точку P(3, 7.5). Следовательно, линейная функция L = 2x1 +2x2 в точке P(3, 7.5) будет иметь наибольшее значение, т.е. максимизируется, и Lmax = 21.
§ Решение примера в электронной математике (Mathcad)
Задаем линейную функцию, которую необходимо максимизировать:

Задаем произвольные начальные условия:

Записываем блок решения, который состоит:

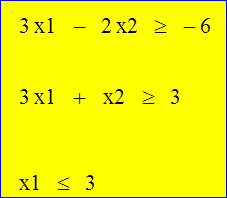

Найдена точка, в которой заданная линейная функция будет иметь наибольшее значение:
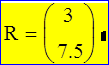
и максимальное значение равно

§ Пример
Минимизировать линейную функцию L = 12x1 + 4x2 при ограничениях:
x1 + x2 ³ 2, x1 ³ ½, x2 £ 4, x1 – x2 £ 0.
Решение.
Задаем линейную функцию
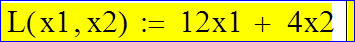
и начальные условия

Блок решения

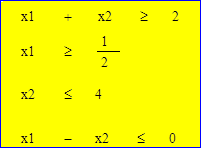

Точка, в которой заданная функция принимает наименьшее значение

Наименьшее значение функции

 2015-05-18
2015-05-18 1656
1656
