Симплекс-метод

Решение основной задачи линейного программирования геометрическим методом достигает наглядности в случае двух или трех переменных. Для большего количества переменных применение геометрического метода становится невозможным.

Так называемый симплекс-метод принадлежит к числу аналитических методов решения основной задачи линейного программирования. Система ограничений в вычислительных методах обычно задается системой линейных уравнений

a₁₁x₁ + a₁₂x₂ + …+ a_1nx_n = b₁

a₂₁x₁ + a₂₂x₂ + …+ a_2nx_n = b₂ (A)

_{…………………………………………….}

a_m1x₁ + a_m2x₂ + …+ a_mnx_n = b_m

И среди неотрицательных решений системы (А) надо найти такие, которые максимизировали линейную функцию

L = c₁x₁ + c₂x₂ + …+ c_nx_n + c₀

§ Пример

Максимизировать линейную форму L = -x₄ + x₅ при ограничениях:

x₁ + x₄ – 2x₅ = 1, x₂ – 2x₄ + x₅ = 3, x₃ + 3x₄ + x₅ = 3

Решение.

Данная система уравнений – совместна, так как ранги матрицы системы

и расширенной матрицы

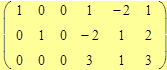совпадают и равны 3.

Следовательно, система уравнений совместна и три переменных (базисных) можно линейно выразить через две свободные переменные. Выразим, например, x₁, x_2, x₃ через x₄ и x₅, т.е. приведем систему к единичному базису

x₁ = 1 – x₄ + x₅

x₂ = 2 + 2x₄ – x_{5 ( C)}

x₃ = 3 – 3x₄ – x₅

Линейную форму L = x₁ + x₄ выразим через свободные переменные x₄ и x₅ (в нашем примере L уже выражено через x₄ и x₅). Теперь при x₄ = 0, x₅ = 0 базисные переменные окажутся равными: x₁ = 1, x₂ = 2, x₃ = 3.

Таким образом, первое допустимое решение системы уравнений есть:

x₁ = 1, x₂ = 2, x₃ = 3, x₄ = 0, x₅ = 0, или (1, 2, 3, 0, 0).

При найденном допустимом решении линейная форма L имеет значение 0, т.е. L₁ = 0.

Теперь попытаемся увеличить значение L₁; увеличение x₄ уменьшит L₁, так как перед x₄ стоит отрицательный коэффициент, а увеличение x₅ дает увеличение и L₁. Увеличим поэтому x₅ так, чтобы x₁, x₂, x₃ не стали отрицательными, оставив x₄ = 0. Из второго уравнения системы (С) видим, что x₅ можно увеличить до 2. Тогда значения переменных будут: x₁ = 5, x₂ = 0, x₃ = 1, x₄ = 0, x₅ = 2, или (5, 0, 1, 0, 2).

Значение линейной формы L при допустимом решении равно L₂ = 2. Величина L при втором шаге увеличилась.

Дальше примем за свободные переменные x₂ и x₄, т.е. именно те переменные, которые в новом решении имеют нулевые значения. С этой целью выразим из второго уравнения системы (С) x₅ через x₂ и x₄. Получим, что x₅ = 2 – x₂ + 2x_4. Тогда

x₁ = 5 – 2x₂ + 3x₄

x₃ = 1 + x₂ – 5 x_{4 (D)}

x₅ = 2 – x₂ + 2x₄

L = 2 – x₂ + x₄

Для увеличения значения L будем увеличивать x₄. Из второго уравнения системы (D) видно, что для неотрицательности x₃ значение x₄ можно довести до x₄ = 1/ 5. При этом условии новое допустимое решение будет:

x₁ = 28 / 5, x₂ = 0, x₃ = 0, x₄ = 1 / 5, x₅ = 12 / 5, или (28/5, 0, 0, 1/5, 12/5).

Значение линейной формы при этом будет L = 11/ 5.

Выразим теперь x₁, x₄, x₅ через свободные переменные x₂ и x₅:

x₁ = 28/5 – 3x₃/5 – 7x₂/5

x₄ = 1/5 – x₃/5 + x₂/5 (E)

x₅ = 12/5 – 2x₃/5 – 3x₂/5

L = 11/5 – x₃ / 5 – 4x₂ / 5.

Так как в последней линейной форме оба свободных переменных входят с отрицательными коэффициентами, то наибольшее значение достигается при

x₂ = 0, x₃ = 0. Это означает, что решение:

x₁ = 28 / 5, x₂ = 0, x₃ = 0, x₄ = 1 / 5, x₅ = 12 / 5, или (28/5, 0, 0, 1/5, 12/5),

является оптимальным и L _max = 11/5.

§ Решение в электронной математике (Mathcad)

Задаем линейную форму

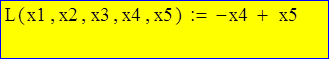
Задаем произвольные начальные условия

Блок решения

Задаем ограничительные условия

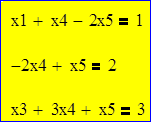
Задаем функцию минимизации

Решение

Присваиваем переменным найденные значения

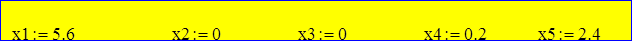
Минимальное значение заданной линейной формы

§ Пример

Цех малого предприятия должен изготовить 100 изделий трех типов, причем каждого вида изделия должно быть произведено не менее 20. При общем запасе металла в 340 кг на производство каждого типа изделий уходит соответственно 4, 3.4 и 2 кг. При общем запасе металла в 700 кг на производство каждого типа изделий уходит соответственно 4.75, 11 и 2 кг. Цена каждого типа изделий по калькуляции соответственно равна: 4, 3 и 2 гривны. Сколько изделий каждого из трех типов необходимо выпустить для максимального объема выпуска в денежном выражении?

Решение.

Обозначим:

x₁ – количество изделий первого типа; x₂ – количество изделий второго типа;

x₃ – количество изделий третьего типа.

Тогда линейная функция, выражающая объем выпуска изделий трех типов в денежном эквиваленте, будет выглядеть следующим образом:

L(x₁, x₂, x₃) = 4x₁ + 3x₂ + 2x₃.

Составим ограничивающие условия:

Так как, каждого изделия должно быть произведено не менее 20 штук, то:

x₁ ³ 20, x₂ ³ 20, x₃ ³ 20.

Так как, при общем запасе металла в 340 кг на производство изделия первого типа уходит 4 кг, второго типа – 3.4 кг, третьего – 2 кг, то:

4x₁ + 3.4x₂ + 2x₃ £ 340.

Так как, при общем запасе в 700 кг на производство изделия первого типа уходит 7.5 кг, второго типа – 11 кг, третьего – 2 кг, то:

7.5x₁ + 11x₂ + 2x₃ £ 700.

Так как, количество произведенных изделий должно быть равно 100, то:

x₁ + x₂ + x₃ = 100.

Решение задачи линейного программирования (т.е. нахождение максимального объема производства изделий трех типов при ограничивающих условиях) в программе Mathcad:

Задается линейная функция

Задаются произвольные начальные условия

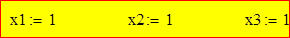
Блок решения

Ограничивающие условия

Задаем операцию максимизации

Полученное решение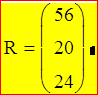

Таким образом, найдено количество изделий каждого типа:

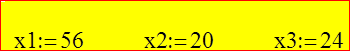
Цена максимально выпускаемой партии изделий трех типов составит:

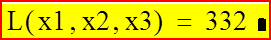
Варианты индивидуальных контрольных заданий №5