Решение. Значения 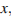при которых определено первое неравенство: 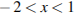и Рассмотрим два случая

Значения при которых определено первое неравенство: и 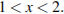Рассмотрим два случая.

Первый случай: 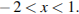Получаем, что 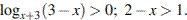Тогда:

Второй случай: 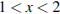. Получаем, что 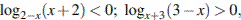следовательно, при 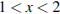неравенство верно.

Ответ:

Задача 5 (17)

Решите неравенство:

Решение.

Сделав замену 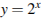, имеем:

Откуда получаем решение неравенства:

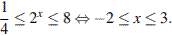
Ответ:

Задача (17)

Решите неравенство:

Решение.

Пусть 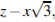получаем:

Возвращаясь к исходной переменной, получаем: 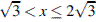или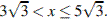

Ответ:

Методика обучения ребенка строевым упражнениям

Средства ЛФК. Классификация физических упражнений в ЛФК и их характеристика

Пара сил. Момент пары сил. Теоремы о парах

Правила хранения, приготовления и использования дезинфицирующих средств

Правила транспортировки биологического материала в лабораторию

Расчёт pH в растворах кислот и оснований. Расчёт концентраций кислот и оснований по pH

Самый сильный аргумент, почему эволюция человека не могла быть