ЕГЭ Профильный уровень №15; № 17
Задача 1(15)
а) Решите уравнение 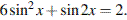
б) Укажите корни данного уравнения, принадлежащие промежутку 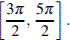
Решение.
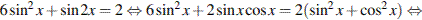
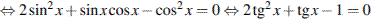 .
.
Отсюда 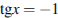 или
или 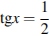 .
.
Если 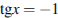 , то
, то 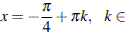
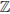 . Если
. Если  , то
, то 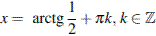 .
.
Из найденных решений промежутку 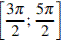 принадлежат числа
принадлежат числа 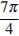 и
и 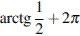 .
.
Ответ: а) 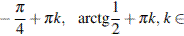
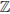 ;
;
б) 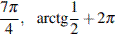 .
.
Задача 2(15)
а) Решите уравнение
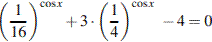
б) Найдите все корни этого уравнения, принадлежащие отрезку 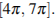
Решение.
Сделаем замену 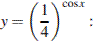
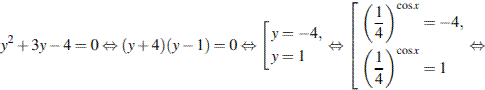
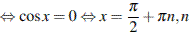
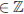
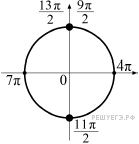 б) При помощи тригонометрической окружности отберём корни, лежащие на отрезке
б) При помощи тригонометрической окружности отберём корни, лежащие на отрезке 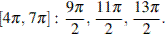
Ответ: а) 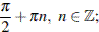 б)
б) 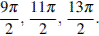
Задача 3(15)
а) Решите уравнение 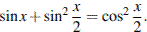
б) Найдите все корни этого уравнения, принадлежащие отрезку 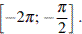
Решение.
а) Перенесем 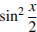 в правую часть и применим формулу для косинуса двойного угла:
в правую часть и применим формулу для косинуса двойного угла:
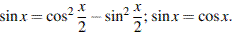
Если 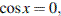 то из уравнения следует, что
то из уравнения следует, что 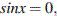 что противоречит основному тригонометрическому тождеству. Поэтому
что противоречит основному тригонометрическому тождеству. Поэтому 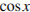 отличен от 0, и не него можно поделить обе части уравнения:
отличен от 0, и не него можно поделить обе части уравнения:
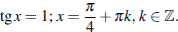
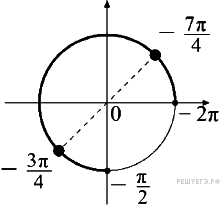
б) При помощи тригонометрической окружности отберём корни уравнения, принадлежащие промежутку 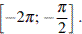 :
:
|
|
|
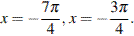
Ответ: а) 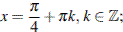 б)
б) 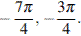
 2015-05-18
2015-05-18 716
716







