В этой лекции рассматриваются матричные игры, не имеющие седловых точек.
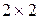 – игры.
– игры.
Рассмотрим игру с платежной матрицей
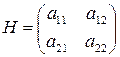
Пусть игрок A применяет набор своих оптимальных стратегий 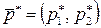 . По основной теореме теории игр это обеспечивает ему выигрыш
. По основной теореме теории игр это обеспечивает ему выигрыш 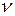 при любых стратегиях игрока В, т.е. выполняются соотношения:
при любых стратегиях игрока В, т.е. выполняются соотношения:
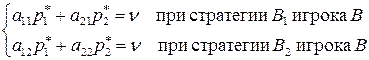 (62)
(62)
Дополняя их уравнением
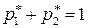 (63)
(63)
получим систему линейных уравнений относительно 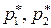 и
и 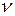 . Решая ее найдем
. Решая ее найдем
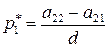 ,
, 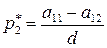 ,
, 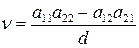 , (64)
, (64)
где 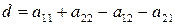 .
.
Повторяя те же рассуждения для игрока В, получим систему линейных уравнений
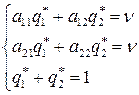 (65)
(65)
Ее решениями будут
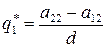 ,
, 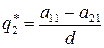 ,
, 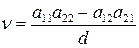 , (66)
, (66)
Пример. Молокозавод поставляет в магазин молочную продукцию (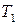 ) и кисломолочную продукцию (
) и кисломолочную продукцию (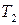 ). Согласно договора между ними продукция поступает в магазин два раза в день: с 10.00 до 11.00 (1-ый срок) и с 17.00 до 18.00 (2-ой срок). Если молокозавод соблюдает сроки поставок, то магазин выплачивает премии по следующей схеме: при поставке продукции
). Согласно договора между ними продукция поступает в магазин два раза в день: с 10.00 до 11.00 (1-ый срок) и с 17.00 до 18.00 (2-ой срок). Если молокозавод соблюдает сроки поставок, то магазин выплачивает премии по следующей схеме: при поставке продукции 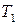 в первый срок выплачивает 5 тыс. руб., во второй срок – 3 тыс. руб.; при поставке продукции
в первый срок выплачивает 5 тыс. руб., во второй срок – 3 тыс. руб.; при поставке продукции 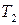 в первый срок выплачивает 2 тыс. руб., во второй срок – 3 тыс. руб. Определить оптимальные стратегии поставок и получения продукции.
в первый срок выплачивает 2 тыс. руб., во второй срок – 3 тыс. руб. Определить оптимальные стратегии поставок и получения продукции.
Решение. Примем молокозавод за игрока А, а магазин – за игрока В. Составим платежную матрицу игры:
| Сроки Продукция | 1-ый срок | 2-ой срок |
 | ||
 |
или
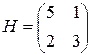
Найдем
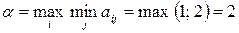
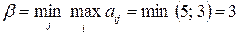 ,
,
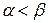 , седловой точки нет. Применим формулы (63) – (65) для определения оптимальных стратегий и цены игры:
, седловой точки нет. Применим формулы (63) – (65) для определения оптимальных стратегий и цены игры:
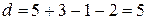 ,
, 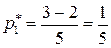 ,
, 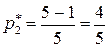 ,
, 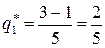 ,
,
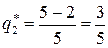 ,
, 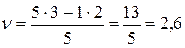 ,
,
Оптимальные стратегии: 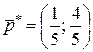 ,
, 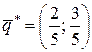 , цена игры
, цена игры 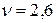 .
.
Таким образом, молокозавод поставляет молочную продукцию с вероятностью 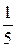 , а кисломолочную продукцию – с вероятностью
, а кисломолочную продукцию – с вероятностью 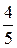 , а магазин получает продукцию в 1-ый срок с вероятностью
, а магазин получает продукцию в 1-ый срок с вероятностью 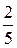 , а во 2-ой срок – с вероятностью
, а во 2-ой срок – с вероятностью 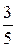 и выплачивает 2,6 тыс. руб. премии молокозаводу ежедневно.
и выплачивает 2,6 тыс. руб. премии молокозаводу ежедневно.
Матричная игра 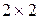 допускает простую геометрическую интерпретацию.
допускает простую геометрическую интерпретацию.
Нахождение цены игры 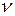 и оптимальной стратегии
и оптимальной стратегии 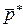 для игрока А равносильно решению уравнения:
для игрока А равносильно решению уравнения:
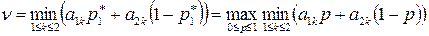 (66)
(66)
Для нахождения правой части (66) применим графический метод.
Пусть игрок А выбрал смешанную стратегию 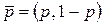 ,
, 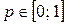 , а игрок В – k -ую чистую стратегию,
, а игрок В – k -ую чистую стратегию, 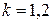 . Тогда средний выигрыш игрока А окажется равным
. Тогда средний выигрыш игрока А окажется равным
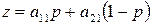 при стратегии
при стратегии 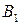 (67)
(67)
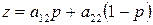 при стратегии
при стратегии 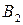 (68)
(68)
Очевидно, 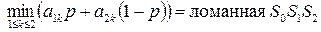 , которую называют нижней огибающей прямых I и II.
, которую называют нижней огибающей прямых I и II.
Нетрудно видеть, что
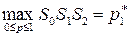
Таким образом, верхняя точка нижней огибающей – 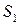 определяет оптимальную стратегию игрока А:
определяет оптимальную стратегию игрока А: 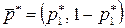 и цену игры
и цену игры 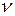 .
.
Проиллюстрируем описанный графичексий метод на рассмотренной выше игре с платежной матрицей 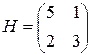 .
.
На плоскости pOz построим две прямые, описываемые уравнениями: 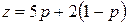 и
и 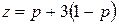 или
или 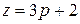 (I) и
(I) и 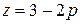 (II).
(II).
Решая систему уравнений
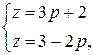
найдем 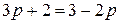 ,
, 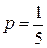 ,
, 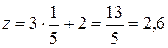 .
.
Таким образом, имеем полученный выше ответ игры: 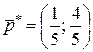 и
и 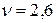 .
.
Теперь покажем как графическим методом найти стратегии игрока В.
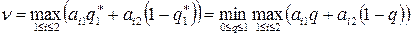 (69)
(69)
Пусть игрок В выбрал смешанную стратегию 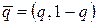 ,
, 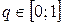 , а игрок А – i -ую чистую стратегию,
, а игрок А – i -ую чистую стратегию, 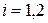 . Тогда средний выигрыш игрока В окажется равным
. Тогда средний выигрыш игрока В окажется равным
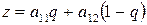 при стратегии
при стратегии 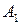 (70)
(70)
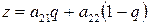 при стратегии
при стратегии 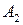 (71)
(71)
Очевидно, 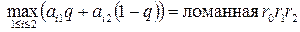 , которую называют верхней огибающей прямых III и IV.
, которую называют верхней огибающей прямых III и IV.
Нетрудно видеть, что
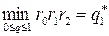
Таким образом, нижняя точка верхней огибающей – 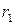 определяет оптимальную стратегию игрока В:
определяет оптимальную стратегию игрока В: 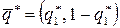 и цену игры
и цену игры 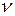 .
.
Для рассмотренной выше гры с матрицей H найдем стратегии игрока В.
На плоскости qOz построим две прямые, описываемые уравнениями: 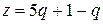 и
и 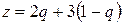 или
или 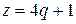 (III) и
(III) и 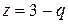 (IV).
(IV).
Решая систему уравнений
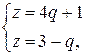
найдем 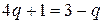 ,
, 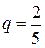 ,
, 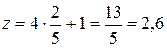 .
.
Таким образом, имеем 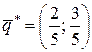 и
и 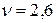 .
.
Замечания. На практике оптимальную стратегию игрока В, если оптимальная стратегия игрока А, следовательно, и цена игры известны, находят приравниванием любого из двух средних выйгрышей игрока В к цене игры:
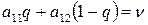 или
или 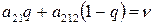 .
.
Для рассмотренного примера такими уравнениями будут
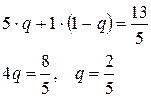 или
или 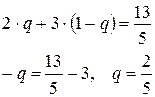
Аналогично находят оптимальную стратегию игрока А, если известна оптимальная стратегия игрока В.
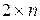 и
и 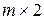 – игры.
– игры.
Решают такие игры графическим способом, описанным выше. Отличие от 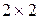 – игр заключается в следующем.
– игр заключается в следующем.
4) Нижняя (верхняя) огибающая семейства прямых
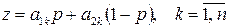
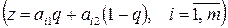
содержит большее число отрезков.
5) Пусть в игре 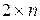 в верхней точке нижней огибающей пересекаются прямые
в верхней точке нижней огибающей пересекаются прямые 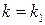 и
и 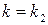 . Тогда при нахождении оптимальной смешанной стратегии игрока В полагают, что
. Тогда при нахождении оптимальной смешанной стратегии игрока В полагают, что 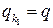 ,
, 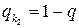 ,
, 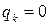 ,
, 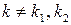 , где q – решение уравнения
, где q – решение уравнения
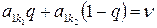 или
или 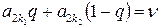
6) Пусть в игре 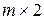 в нижней точке верхней огибающей пересекаются прямые
в нижней точке верхней огибающей пересекаются прямые 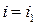 и
и 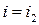 . Тогда при нахождении оптимальной смешанной стратегии игрока А полагают, что
. Тогда при нахождении оптимальной смешанной стратегии игрока А полагают, что 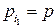 ,
, 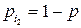 ,
, 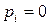 ,
, 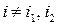 , где p – решение уравнения
, где p – решение уравнения
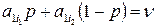 или
или 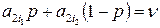 .
.
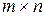 – игры.
– игры.
При решении таких игр рекомендуется предварительно уменьшить размеры платежной матрицы или упростить ее в некотором смысле. С этой целью применяют следующие правила.
Правило доминировнаия.
Из платежной матрицы исключают чистые стратегии заведомо невыгодные по сравнению с другими:
а) для игрока А такими стратегиями являются те, которым соответствуют строки с элементами не большими по сравнению с элементами других строк;
б) для игрока В такими стратегиями являются те, которым соответствуют столбцы с элементами не меньшими по сравнению с элементами других столбцов.
Например, рассмотрим игру с матрицей
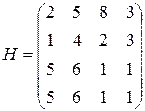
Сравнивая строки, убеждаемся, что элементы 2-ой строки не больше соответствующих элементов 1-ой строки, а 3-ья строка совпадает с 4-ой. Следовательно, стратегии 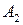 и
и 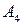 невыгодные и могут быть отброшены. Матрица игры преобразуется к матрице
невыгодные и могут быть отброшены. Матрица игры преобразуется к матрице
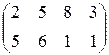
Сравнивая столбцы полученной матрицы, убеждаемся, что элементы 2-го столбца не меньше соответствующих элементов 1-го столбца, а элементы 3-го столбца не меньше соответствующих элементов 4-го столбца, т.е. стратегии 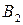 и
и 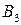 также могут быть отброшены. Окончательно усеченная матрица игры имеет вид
также могут быть отброшены. Окончательно усеченная матрица игры имеет вид
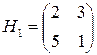 .
.
Таким образом, оптимальными стратегиями игроков А и В игры с матрицей Н будут 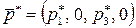 и
и 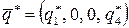 , где
, где 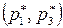 и
и 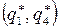 – оптимальные стратегии игры с матрицей
– оптимальные стратегии игры с матрицей 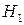 .
.
Аффинное правило.
Пусть 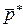 и
и 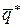 – оптимальные смешанные стратегии игроков А и В в игре с платежной матрицей
– оптимальные смешанные стратегии игроков А и В в игре с платежной матрицей 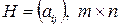 и ценой
и ценой 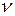 . Тогда
. Тогда 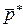 и
и 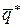 будут оптимальными стратегиями и в игре с матрицей
будут оптимальными стратегиями и в игре с матрицей 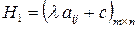 и ценой
и ценой 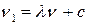 .
.
Например, игру с матрицей 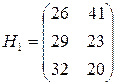 можно заменить игрой с матрицей
можно заменить игрой с матрицей 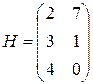 , т.к. элементы этих матриц связаны соотношениями
, т.к. элементы этих матриц связаны соотношениями 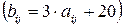 :
: 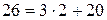 ;
; 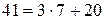 ;
; 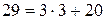 ;
; 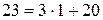 ;
; 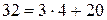 ;
; 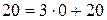 . При этом оптимальные стратегии игр совпадают, а цены игр связаны соотношением
. При этом оптимальные стратегии игр совпадают, а цены игр связаны соотношением 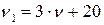 .
.
В общем случае решение игр размера 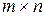 в смешанных стратегиях сводят к решению двух возможно двойственных ЗЛП.
в смешанных стратегиях сводят к решению двух возможно двойственных ЗЛП.
Редукция матричных игр к ЗЛП.
Пусть игра 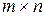 задана платежной матрицей
задана платежной матрицей 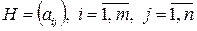 . Через
. Через 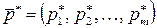 и
и 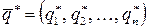 обозначим соответственно оптимальные стратегии игроков А и В. Пусть
обозначим соответственно оптимальные стратегии игроков А и В. Пусть 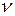 – цена игры. Не умаляя общности, полагаем
– цена игры. Не умаляя общности, полагаем 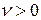 . В противном случае с помощью аффинного правила добьемся того, что все
. В противном случае с помощью аффинного правила добьемся того, что все 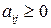 .
.
Оптимальная стратегия стратегия игрока А обеспечивает ему средний выигрыш, не меньший 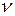 , при любой стратегии игрока В. Поэтому все средние выигрыши игрока А можно выписать в виде системы неравенств:
, при любой стратегии игрока В. Поэтому все средние выигрыши игрока А можно выписать в виде системы неравенств:
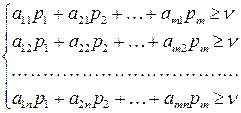 (72)
(72)
Введем новые переменные:
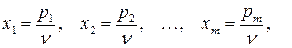 (73)
(73)
Тогда после деления каждого неравенства из (71) на  получим новую систему неравенств
получим новую систему неравенств
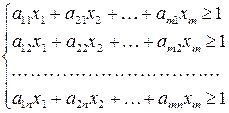 (73)
(73)
Из равенства
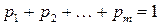
нетрудно получить соотношение для 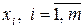 :
:
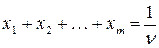 .
.
Игрок А стремится максимизировать свой гарантированный выигрыш 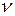 . Максимизация
. Максимизация 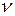 равносильна минимизации
равносильна минимизации 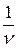 . Следовательно, получили следующую задачу для нахождения оптимальной стратегии игрока А:
. Следовательно, получили следующую задачу для нахождения оптимальной стратегии игрока А:
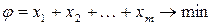 (74)
(74)
при условиях (73) и
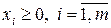 (75)
(75)
Сформулированная задача (74) – (76) является ЗЛП.
Повторим с естественными изменениями предыдущие рассуждения для определения оптимальной стратегии игрока В.
Игрок В стремиться минимизировать гарантированный проигрыш 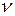 . Все средние проигрыши игрока В запишем в виде системы неравенст:
. Все средние проигрыши игрока В запишем в виде системы неравенст:
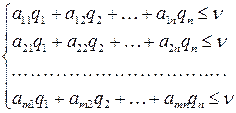 , (76)
, (76)
которые следуют из того, что средний проигрыш игрока В не превосходит цены игры 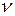 при любой стратегии игрока А.
при любой стратегии игрока А.
В обозначениях
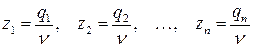
система неравенств (76) примет вид
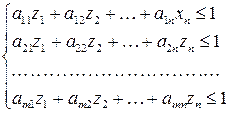 (77)
(77)
Применение  удовлетворяют соотношению
удовлетворяют соотношению
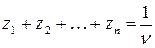 .
.
Минимизация 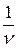 равносильна максимизации
равносильна максимизации 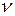 .
.
Получили следующую задачу для нахождения оптимальной стратегии игрока В:
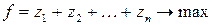 (78)
(78)
при условиях (77) и
 (79)
(79)
Задача (77) – (79) также является ЗЛП.
Таким образом, игра 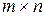 свелась к двум ЗЛП, которые запишем в матричном виде
свелась к двум ЗЛП, которые запишем в матричном виде
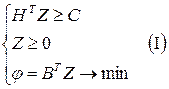
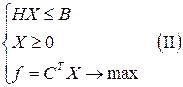
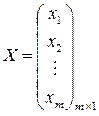 ,
,  ,
,  ,
, 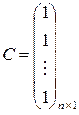
Очевидно, задачи I и II являются двойственными ЗЛП.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. А.В. Соколов, В.В. Токарев. Методы оптимальных решений. Т.1. Общие положения. Математическое программирование. Москва: ФИЗМАТЛИТ, 2010.
2. А.В. Соколов, В.В. Токарев. Методы оптимальных решений. Т.2. Многокритериальность. Динамика. Неопределенность. Москва: ФИЗМАТЛИТ, 2010.
3. Конюховский П.В. Математические методы исследования операций в экономике. СПб.: Питер, 2000.
4. М. Интрилигатор. Математические методы оптимизации и экономическая теория. М.: Изд. Айрис-Пресс, 2002.
5. Ф.П. Васильев. Методы оптимизации. М. Факториал Пресс, 2005.
ОГЛАВЛЕНИЕ
| Введение …………………………………………………………………….. | |
| ЛЕКЦИЯ 1. Исследование операций. Экономико-математические модели. ………………………………………………………………………. | |
| ЛЕКЦИЯ 2. Балансовые модели. Модель Леонтьева многоотраслевой экономики. Продуктивные модели…………………………………………. | |
| ЛЕКЦИЯ 3,4,5. Задачи математического и линейного программирования. Модели линейного программирования……………... | |
| ЛЕКЦИЯ 6. Динамическое программирование. Принцип оптимальности и функциональности. Функциональное уравнение Беллмана……………. | |
| ЛЕКЦИЯ 7. Модели потребительского выбора. Функция полезности. Линии безразличия. Оптимизация функции полезности. Функции спроса и предложения………………………………………………………. | |
| ЛЕКЦИЯ 8. Элементы теории игр в задачах оптимального управления экономическими процессами………………………………………………. | |
| ЛЕКЦИЯ 9. Методы решения матричных игр в смешанных стратегиях... | |
| СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ …………………………… |
Учебное издание
Г. Н. Камышова,
Н. Н. Терехова
МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ
Краткий курс лекций
Издается в авторской редакции
Корректура авторов
 2015-05-18
2015-05-18 1208
1208