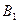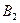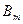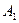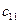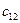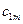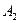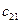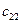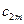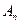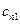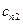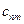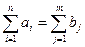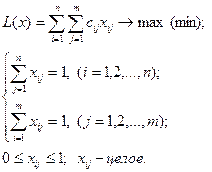В рассмотренных в предыдущем параграфе моделях, «соперник» ЛПР, который мы называли «состоянием природы», ни как не реагировал на возможные решения ЛПР, то есть последний был ему совершенно безразличен. Однако часто таким соперником является мыслящий субъект или их группа, который осознанно выбирает вариант реализации ситуации.
Рассмотрим следующую модель. ЛПР А желает принять решение, на результат которого влияет другое ЛПР В, цели которого противоположны А. ЛПР В анализирует все возможные варианты А и принимает такое решение, которое приводит к наименьшему выигрышу А (соответственно максимальному своему выигрышу). Примерами таких ситуаций служат отношения между продавцом и покупателем, адвокатом и прокурором, кредитором и дебитором, истцом и ответчиком и т.д. Подобные ситуации называются конфликтными. Математические методы анализа конфликтных ситуаций объединяются под названием теории игр, сама конфликтная ситуация носит название игры, а стороны, участвующие в конфликте, называются игроками. Исход игры называется выигрышем (или проигрышем) игроков. Если выигрыш одного игрока равен проигрышу другого, то игра называется антагонистической. Пусть игрок А может выбрать в качестве действий одну из п альтернатив: А 1, А 2,…, Аn. Эти альтернативы в теории игр принято называть стратегиями. Аналогично, игрок В может принять одну из m стратегий В 1, В 2,…, Вm. Предположим, что известны выигрыши (проигрыши) игрока А при любой выбранной им стратегии Аi и любом ответе ему игроком В – стратегии Вj. Пусть этот результат выражен числом аij (которое может быть и отрицательным в случае проигрыша А). Величины аij образуют матрицу:
| Ai Bj | В 1 | В 2 | … | Вm |
| А 1 | a 11 | a 12 | … | a 1 m |
| А 2 | a 21 | a 21 | … | a 2 m |
| … | … | |||
| Аn | an 1 | an 2 | … | anm |
Эта матрица называется платежной или матрицей игры.
Рассмотрим игру со стороны А. Он, выбирая свою стратегию Аi, понимает, что В ответит ему такой стратегией Вj, чтобы выигрыш А был минимальным. Поэтому, из всех наихудших вариантов (минимальных элементов каждой строки платежной матрицы) 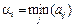 , игроку А выгодно выбрать стратегию, соответствующую максимальному из этих элементов:
, игроку А выгодно выбрать стратегию, соответствующую максимальному из этих элементов:
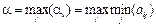 .
.
Величина a называется нижнейценой игры или максимином. Это гарантированный выигрыш игрока А. С другой стороны, игрок В выбирая свою стратегию В j понимает, что игрок А ответит такой стратегией Аi, чтобы его выигрыш был максимален. Поэтому из наилучших вариантов для А (максимальных элементов каждого столбца) 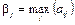 игроку В рационально выбрать свою стратегию, соответствующую минимальному из этих чисел:
игроку В рационально выбрать свою стратегию, соответствующую минимальному из этих чисел:
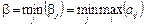 .
.
Величина b называется верхней ценой игры или минимаксом. Это максимальный проигрыш игрока В. Реальный результат решения конфликтной ситуации, называемый ценой игры n, заключен между верхней и нижней ценой: 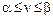 . В случае, если верхняя и нижняя цены совпадают
. В случае, если верхняя и нижняя цены совпадают 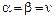 , то игра имеет решение в чистых стратегиях, то есть можно точно определить стратегии
, то игра имеет решение в чистых стратегиях, то есть можно точно определить стратегии 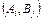 , которые выгодны для обоих сторон. Если одна сторона отойдет от своей оптимальной стратегии, то ее выигрыш от этого только уменьшится.
, которые выгодны для обоих сторон. Если одна сторона отойдет от своей оптимальной стратегии, то ее выигрыш от этого только уменьшится.
Пример: Дебитор А желает выбрать один из четырех условий займа: А 1, А 2, А 3, А 4. Кредитор может на любой вариант займа ответить вариантом предоставления кредита В 1, В 2, В 3, В 4, В 5. Процентные ставки для дебитора при любом варианте кредитора представлены платежной матрицей:
| Ai Bj | В 1 | В 2 | В 3 | В 4 | В 5 |
| А 1 | |||||
| А 2 | |||||
| А 3 | |||||
| А 4 |
Находим минимальные элементы каждой строки платежной матрицы a I и из них находим максимальное значение. Из максимальных элементов каждого столбца b j выбираем минимальный.
| Ai Bj | В 1 | В 2 | В 3 | В 4 | В 5 | a i |
| А 1 | 1 | |||||
| А 2 | 5 | |||||
| А 3 | 2 | |||||
| А 4 | 2 | |||||
| b j | 9 | 7 | 8 | 5 | 8 |
Видно, что верхние и нижние цены игры совпадают 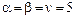 , следовательно для обоих игроков выгодны стратегии
, следовательно для обоих игроков выгодны стратегии 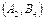 и процентная ставка, равная 5. При принятии игроками иной стратегии, отличной от оптимальной, этот игрок только проиграет.
и процентная ставка, равная 5. При принятии игроками иной стратегии, отличной от оптимальной, этот игрок только проиграет.
Рассмотрим теперь ситуацию, когда верхняя и нижняя цены не совпадают 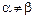 . В этом случае игра решается в смешанных стратегиях. Смешанный стратегии предполагают, что каждый игрок будет выбирать случайно из возможно допустимых чистых стратегий (но выбирать их с вероятностями), либо частично реализовывать чистые стратегии в заданных пропорциях. Нахождение этих вероятностей (или пропорций) и является решением игры. Таким образом, в общем виде, решением игры являются смешанные стратегии
. В этом случае игра решается в смешанных стратегиях. Смешанный стратегии предполагают, что каждый игрок будет выбирать случайно из возможно допустимых чистых стратегий (но выбирать их с вероятностями), либо частично реализовывать чистые стратегии в заданных пропорциях. Нахождение этих вероятностей (или пропорций) и является решением игры. Таким образом, в общем виде, решением игры являются смешанные стратегии 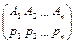 и
и 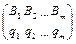 , где
, где 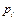 и
и 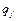 - вероятности чистых стратегий
- вероятности чистых стратегий 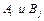 в смешанной.
в смешанной.
Рассмотрим сначала простейший случай игры, решаемой в смешанных стратегиях – игру 2х2, когда у каждого игрока имеется лишь по две стратегии. Платежная матрица такой игры есть:
| Ai Bj | B 1 | B 2 |
| A 1 | a 11 | a 12 |
| A 2 | a 21 | a 22 |
Решение игры 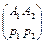 и
и 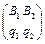 , где
, где 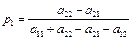 ,
, 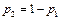 ,
, 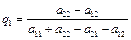 ,
, 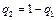 . Цена игры равна
. Цена игры равна 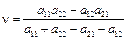 .
.
Пример. Игрок А прячет в одной из рук монету. Игрок В пытается угадать руку с монетой. Если В не угадывает, то А получает от В 1 у.е. Если В угадывает руку с монетой и эта рука правая, то он получает от А 1 у.е. Если В находит монету в левой руке, то он получает от А 2 у.е. Определить оптимальные стратегии поведения для каждого игрока и средний выигрыш для А.
Пусть стратегии игроков: А 1 – спрятать в правой; В 1 – искать в правой; А 2 – спрятать в левой; В 2 – искать в левой. Игровая матрица для данной ситуации относительно игрока А имеет вид:
| Ai Bj | B 1 | B 2 |
| A 1 | -1 | |
| A 2 | -2 |
Тогда вероятности чистых стратегий в смешанной равны:
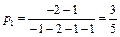 ,
, 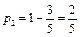 ,
, 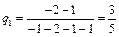 ,
, 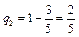 . Цена игры равна
. Цена игры равна 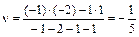 .
.
Таким образом, игроку А нужно случайно чередовать руки с монетой, но в правой руке прятать в среднем в трех случаях из пяти, а в левой в двух случаях из пяти. В это случае в каждой игре в среднем А получит (-1/5) руб., то есть теряет 20 коп., игра для А не выгодная. Для игрока В выгодно также чередовать руки в которых он ищет монету, но в правой руке искать в 3 случаях из 5, что приведет к среднему выигрышу для него в 20 коп. за игру.
В некоторых случаях удается аналогичным образом решить и игровые ситуации с платежными матрицами, большего размера, упростив их до игры 2х2. При этом используются следующие правила:
1) Если все элементы какой-либо строки платежной матрицы не превышают соответствующих элементов любой другой строки, то строка с меньшими элементами соответствует стратегии, которая для игрока А заведомо не выгодна при любом ответе игрока В. Поэтому из платежной матицы строку с меньшими элементами можно вычеркнуть, тем самым выведя из рассмотрения соответствующую ей стратегию.
2) С другой стороны, для игрока В невыгодна заранее, независимо от ответа А, стратегия, которой соответствует столбец платежной матрицы, у которого все элементы больше или равны соответствующим элементам любого другого столбца. Столбец с большими элементами также можно вывести из рассмотрения, вычеркнув из платежной матрицы.
Пример.
Директор транспортной компании А, оказывающей транспортные услуги по перевозке пассажиров в областном центре, планирует открыть один или несколько маршрутов: А1, А2, А3 и А4. Для этого было закуплено 100 микроавтобусов. Он может поставить весь транспорт на одном из маршрутов (наиболее выгодном), либо распределить по нескольким маршрутам. Спрос на транспорт, а соответственно и прибыль компании во многом зависит от того, какие маршруты в ближайшее время откроет главный конкурент - компания В. Ее руководство полностью владеет ситуацией и может открыть несколько из пяти маршрутов В1, В2, В3, В4 и В5. Оценки прибыли компании А (млн. руб.) при любом ответе В представлена платежной матрицей:
| А i B j | В1 | В2 | В3 | В4 | В5 |
| А1 | |||||
| А2 | |||||
| А3 | |||||
| А4 |
Находим оптимальное распределение прибыли по маршрутам и ожидаемую прибыль.
Вычеркиваем из таблицы второй столбец, т.к. все его элементы больше или равны элементам третьего. Вычеркиваем четвертую строку, т.к. ее оставшиеся элементы меньше элементов третьей. Элементы первого столбца больше элементов третьего, вычеркиваем первый столбец. Вторую строку вычеркиваем в результате сравнения с первой. Четвертый столбец вычеркиваем после сравнения с третьим. В результате получаем матрицу:
| А i B j |  В1 В1 | В2 | В3 | В4 | В5 |
| А1 | |||||
| А2 | |||||
| А3 | |||||
| А4 |
которая эквивалентна матрице:
| A i B j | B3 | B5 |
| A1 | ||
| A3 |
Тогда вероятности чистых стратегий компании А в смешанной 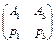 равны:
равны: 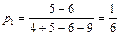 ,
, 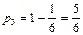 . Цена игры равна
. Цена игры равна 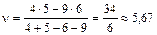 . Следовательно, 1/6 часть автопарка (17 машин) нужно направить на маршрут А1, а остальные 5/6 парка (83 машины) на маршрут А3. Маршруты А2 и А4 использовать не рационально. При этом прибыль, не зависимо от ответа компании В будет составлять 34/6 млн. руб.
. Следовательно, 1/6 часть автопарка (17 машин) нужно направить на маршрут А1, а остальные 5/6 парка (83 машины) на маршрут А3. Маршруты А2 и А4 использовать не рационально. При этом прибыль, не зависимо от ответа компании В будет составлять 34/6 млн. руб.
Рассмотрим случай, когда платежную матрицу нельзя упростить до размера 2х2. Пусть упрощенная платежная матрица имеет вид: 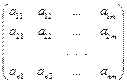 . Тогда для нахождения вероятностей
. Тогда для нахождения вероятностей 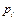 и
и 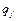 смешанных стратегий
смешанных стратегий 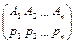 и
и 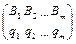 , необходимо решать прямую и двойственную задачи линейного программирования вида:
, необходимо решать прямую и двойственную задачи линейного программирования вида:
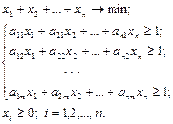
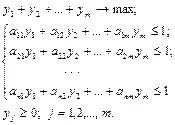
Из решения задач линейного программирования находятся цена игры 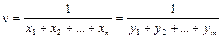 и вероятности состояний
и вероятности состояний 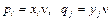 .
.
Пример. Построить прямую и двойственную задачи линейного программирования для решения матричной игры, заданной платежной матрицей: 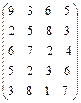 .
.
Прямая и двойственная задачи линейного программирования имеют вид:
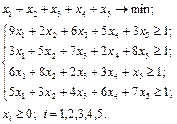
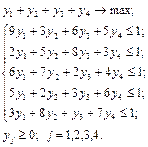
Из решения можно найти игры цену игры 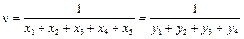 и вероятности состояний
и вероятности состояний 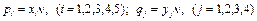 .
.
Известно, что решение задач линейного программирования связано с громоздкими вычислениями. Для численного решения этих задач можно использовать надстройку пакета прикладных программ MS Excel «Поиск решения», которая входит в MS Office.
Методы решения задач принятия решений в условиях конфликта с использованием ЭВМ приведены в лабораторной работе № 3 данного пособия.
|
Задача о назначениях является частным случаем общих классов оптимизационных задач, и поэтому существует много разнообразных методов ее решения. История решения задачи о назначениях показывает, как постепенно математики приходили к пониманию вычислительной сложности методов, как далеко не сразу была осознана необходимость поиска эффективных алгоритмов, удобных для практического применения. Впервые задача о назначениях была рассмотрена Гаспаром Монжем (1746-1818) в 1784 году в геометрической форме. Монж рассматривает задачу о перевозке земли с одного участка на другой, с той же площадью. При этом земля на участке рассматривается как множество «молекул» разного веса, и ставится задача выбора такого способа транспортировки, при котором суммарное перемещение молекул будет минимальным. Монж предложил геометрический способ решения задачи: перемещать молекулы по прямым, касательным к обеим областям. Позднее, в начале XX века, была показана некорректность решения Монжа. Следующие шаги в решении задачи о назначениях относятся к первой трети XX века и связаны с именами Кёнига и Эгервари.
Задача о назначениях может быть переформулирована как задача поиска совершенного паросочетания минимального веса во взвешенном двудольном графе. При этом вершины графа соответствуют строкам и столбцам матрицы стоимостей, а ребра имеют веса, равные элементам матрицы [3]. Кёниг доказал теорему о том, что максимальный размер паросочетания совпадает с размером минимального вершинного покрытия, а Эгервари впервые рассмотрел паросочетание во взвешенном графе и доказал теорему для оценки максимальной суммы весов ребер в паросочетании. Доказательство теоремы содержало алгоритм, позволяющий путем последовательного преобразования матрицы найти эту сумму. Работы Кёнига и Эгервари стали основой для «венгерского» метода решения задачи о назначениях, разработанного Куном в 50-х годах. В конце 40-х годов XX века были созданы первые ЭВМ. Задача о назначениях была в ряду первых задач, которые решались с помощью компьютера. Развитие вычислительной техники привело к бурному развитию методов оптимизации. Тем временем, в 1947 году Данциг предложил очень эффективный метод для решения общей задачи линейного программирования, получивший название симплекс-метод. Задача о назначениях может быть легко сведена к задаче линейного программирования, если ввести для каждого элемента матрицы стоимостей свою переменную, принимающую значения 0 или 1, и записать 2n ограничений, что в каждом столбце и каждой строке сумма элементов строго равна единице.
В 1955 году Кун опубликовал первый аналитический алгоритм решения задачи о назначениях – венгерский метод.
Венгерский метод Куна состоит из трех шагов:
Шаг 1. Редукция матрицы.
В исходной матрице стоимостей в каждой строке определяется минимальная стоимость и вычитается от всех элементов строки. В полученной матрице в каждом столбце определяется минимальная стоимость и вычитается от всех элементов столбца. В результате, в каждой строке и в каждом столбце матрицы появятся нулевые элементы.
Шаг 2. Построение паросочетания.
Строится двудольный граф, вершины которого соответствуют строкам и столбцам матрицы, а ребра – нулевым элементам, стоящим на пересечении соответствующих строк и столбцов. Ищется наибольшее паросочетание в построенном графе. Если паросочетание окажется полным, то оно задает оптимальное решение задачи о назначениях, иначе выполняется шаг 3.
Шаг 3. Преобразование Эгервари.
В последней матрице проводится минимальное число горизонтальных и вертикальных прямых по строкам и столбцам так, чтобы в матрице вычеркнулись все нулевые элементы. Наименьший невычеркнутый элемент вычитается из всех невычеркнутых элементов и прибавляется к элементам, стоящим на пересечении проведенных прямых. В результате в матрице количество нулевых элементов увеличится.
Далее снова выполняется шаг 2.
Рассмотрим ПРИМЕР.
Решить задачу об оптимальном назначении с матрицей затрат A:
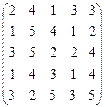
Так, как имеется матрица затрат, то решается задача на минимум. Решение будем искать венгерским методом.
Этап 1. В каждой строке ищем минимальный элемент (он взят в круглые скобки):
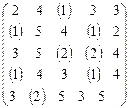 ;
;
и отнимаем эти числа от всех элементов строки. Получим:
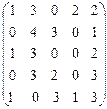
Теперь проводим аналогичную процедуру для всех столбцов: ищем наименьший элемент по столбцу и отнимаем его из всех элементов столбца. Получим:
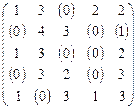 ;
; 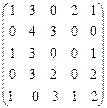 .
.
Этап 2. Выбираем строку с одним нулем (строка №1), выделяем нуль жирным и зачеркиваем (обозначим символом Ø) оставшиеся нулевые значения этого столбца (столбца №3). Выбираем строку с одним нулевым значением (строка №5), выделяем нуль. Выбираем строку с одним нулем (строка №3), выделяем нуль жирным и зачеркиваем оставшиеся нулевые значения этого столбца (столбца №4). Выбираем строку с одним нулем (строка №4), выделяем нуль жирным и зачеркиваем оставшиеся нулевые значения этого столбца (столбца №1). Выбираем строку с одним нулевым значением (строка №2), выделяем нуль. Получаем оптимальную матрицу назначений:
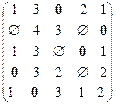 .
.
По выделенным жирным шрифтом нулям определяем решение задачи о назначениях: 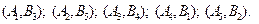 Минимальное значение целевой функции: 1+2+2+1+2=8. В лабораторном практикуме приводится метод решения задачи о назначениях на ЭВМ.
Минимальное значение целевой функции: 1+2+2+1+2=8. В лабораторном практикуме приводится метод решения задачи о назначениях на ЭВМ.
 2015-02-14
2015-02-14 2093
2093

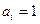 – единичное количество ресурса
– единичное количество ресурса 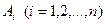 , например: один работник; одно
, например: один работник; одно 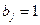 – единичное количество работы
– единичное количество работы 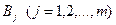 , например: одна должность; один маршрут; одна лаборатория. 4.
, например: одна должность; один маршрут; одна лаборатория. 4. 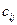 –
– 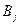 с помощью ресурса
с помощью ресурса 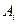 . Например, компетентность i -го работника при работе на j -й должности; время, за которое i -е
. Например, компетентность i -го работника при работе на j -й должности; время, за которое i -е 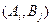 . В качестве исходных данных введем переменные
. В качестве исходных данных введем переменные 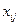 – факт назначения или неназначения ресурса
– факт назначения или неназначения ресурса 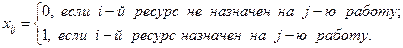 Также имеется некоторая целевая функция
Также имеется некоторая целевая функция 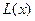 , равная общей (суммарной) характеристики качества распределения ресурсов по работам. Это может быть прибыль или процент брака, издержки или
, равная общей (суммарной) характеристики качества распределения ресурсов по работам. Это может быть прибыль или процент брака, издержки или