С учетом (1):
| Виды сырья | Затраты сырья (ед.) на производство 1 единицы продукции | Запасы сырья | |
| Р1 | Р2 | ||
| S1 | |||
| S2 | |||
| S3 | |||
| Прибыль от реализации 1 ед. прод. | |||
| План пр-ва (ед. прод.) | x1 | x2 |
1. Математическая модель задачи: (и), предполагая, что оптимальным считается план производства, обеспечивающий максимально возможную прибыль от реализации продукции.
– система ограничений:
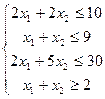 (2)
(2)
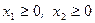
– целевая функция: 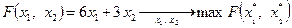 (3)
(3)
Т.о., необходимо при заданных ограничениях (2) найти значения переменных х1 и х2, при
которых целевая функция F принимает максимальное значение.
2. На плоскости Оx 1 x 2 построить область допустимых решений и найти оптимальное решение (оптимальный план производства) геометрическим методом.
Решение.
Преобразуем исходную систему:
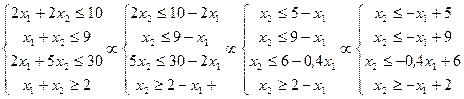
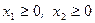 .
.
Строим область допустимых планов ЗЛП, графически решая систему неравенств с учетом двух последних неравенств при помощи табличного процессора MS Excel (см. рис. 1)
Таблица 1.1
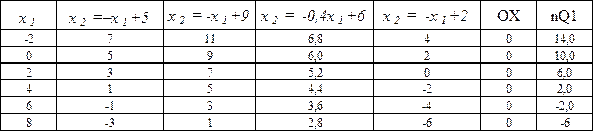
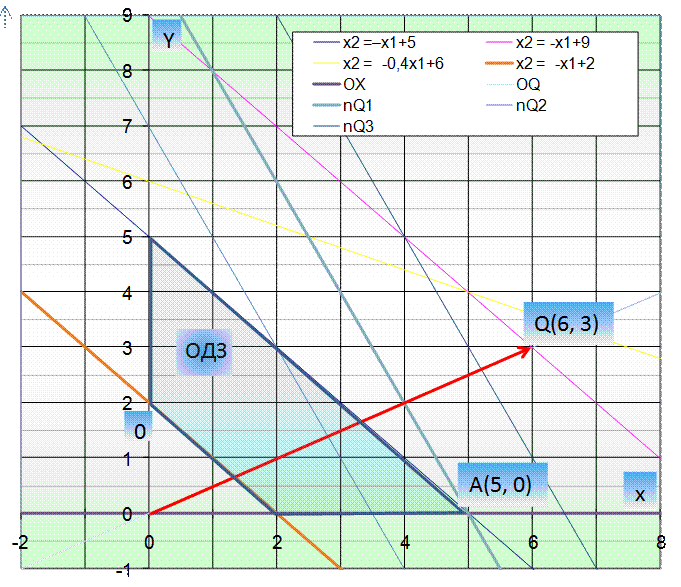
Рисунок 1.
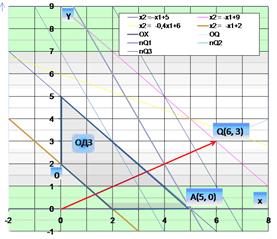
Координаты угловых точек области допустимых значений ОДЗ (5;0); (2;0), (0,2) и (0;5) определяются по графику как координаты точек пересечения граничных линий области допустимых планов.
Cтроим вектор градиента целевой функции F: gradQ 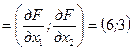 , координаты которого равны соответствующим коэффициентам при x 1 и x 2 в выражении целевой функции F. После этого проводим семейство nQ1, nQ2, nQ3 линий уровня целевой функции F перпендикулярных вектору градиента Q:
, координаты которого равны соответствующим коэффициентам при x 1 и x 2 в выражении целевой функции F. После этого проводим семейство nQ1, nQ2, nQ3 линий уровня целевой функции F перпендикулярных вектору градиента Q: 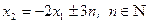 .
.
Целевая функция 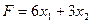 достигает своего максимума, если двигать линию уровня параллельно самой себе в направлении grad Q. При этом линия уровня выходит из области допустимых планов угловой точке А(5;0). Следовательно, план x1,2* =(5;0) является оптимальным в решаемой ЗЛП на максимум.
достигает своего максимума, если двигать линию уровня параллельно самой себе в направлении grad Q. При этом линия уровня выходит из области допустимых планов угловой точке А(5;0). Следовательно, план x1,2* =(5;0) является оптимальным в решаемой ЗЛП на максимум.
x 1max* = 5; x 2max* =0; F max = 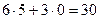 .
.
Ответ: xmax * = (5;); F max = 30.
 2015-05-18
2015-05-18 314
314








