Решение. Стержень квадратного поперечного сечения со стороной квадрата равной и длиной изготовлен из изотропного упругого материала с модулем упругости

Задача 1

Стержень квадратного поперечного сечения со стороной квадрата равной 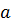и длиной 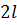изготовлен из изотропного упругого материала с модулем упругости 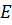и коэффициентом Пуассона 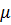. Стержень вставляется в паз, сделанный точно по его размерам (см. рис.1.1).

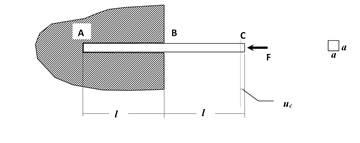Рис.1.1

Материал, в котором сделан паз, следует считать абсолютно жестким. Трение по поверхности касания стержня и паза отсутствует. Определить перемещение точки С, которое вызовет приложение силы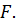

Решение.

На участке А - В материал стержня не может расширяться в поперечном направлении, поэтому в стержне появятся поперечные напряжения, напряженное состояние здесь будет трехосным (см. рис. 1.2). 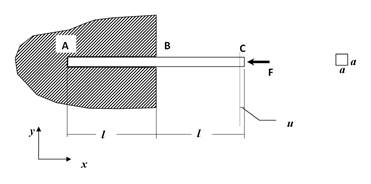Рис. 1.2

Запишем обобщенный закон Гука для трехосного напряженного состояния:

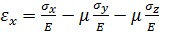
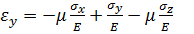(1)

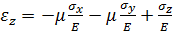
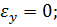
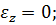
В нашем случае 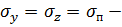поперечное напряжение. Подставляя эти значения в обобщенный закон Гука, получим:

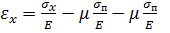
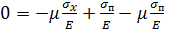(2)

.

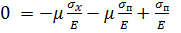Из второй или из третьей строки уравнений (2) получим 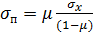. Подставляя вместо 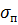полученное значение в первую строку уравнений (2), получим:

= .

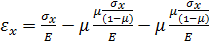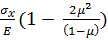Итак, получено выражение 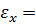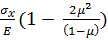., которое связывает продольное напряжение в стержне с продольной деформацией в условиях, когда поперечная деформация стеснена. Как видно деформация в этом случае получается несколько меньшей, чем в случае одноосного растяжения стержня. Поскольку по условию задачи трение по поверхности касания отсутствует, то во всех поперечных сечениях стержня продольная сила будет равна - F (стержень испытывает сжатие вдоль оси x), соответственно напряжение сжатия окажется равным 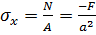. Теперь для участка стержня А-В величина продольной деформации получится равной:

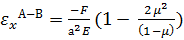. Умножая относительную деформацию на первоначальную длину участка, получим .

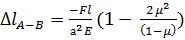Для участка В-С все значительно проще, так как здесь имеем обыкновенное одноосное сжатие 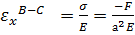, соответственно .

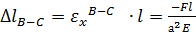Поскольку левое сечение неподвижно, искомое смещение сечения С (см. рис. 1.2)будет равно сумме удлинений обоих участков стержня.

.

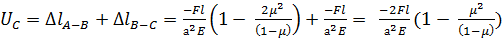Знак минус указывает на то, что участки стержня укорачиваются, следовательно сечение С перемещается налево. Ответ: Перемещение сечения С равно: 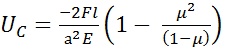, сечение смещается налево.