По условию требуется минимизировать функцию 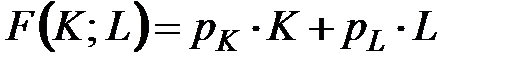 =
= 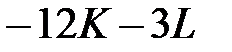 при ограничениях:
при ограничениях:
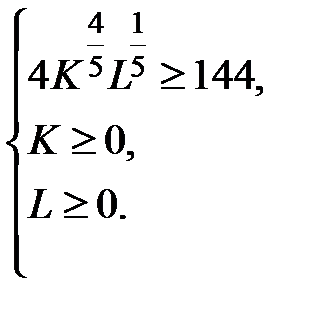 или
или 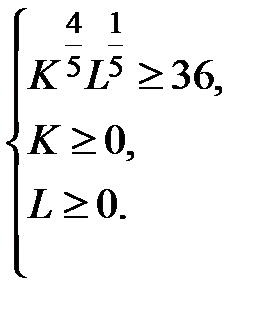
Для применения теоремы Куна-Таккера проверим вогнутость нелинейной функции 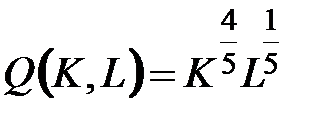 . Предварительно вычисляем производные:
. Предварительно вычисляем производные: 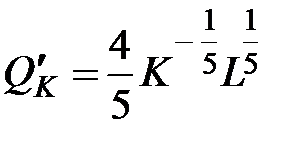 ,
, 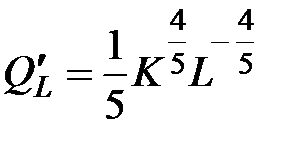 ,
, 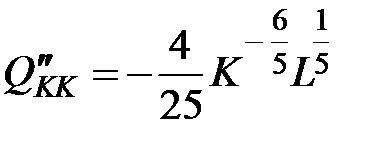 ,
, 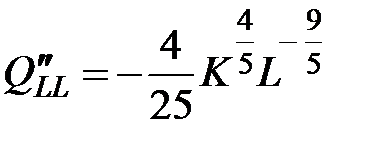 ,
, 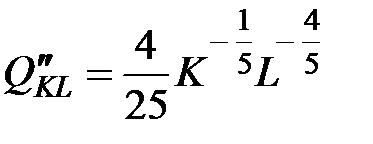 .
.
Тогда второй дифференциал 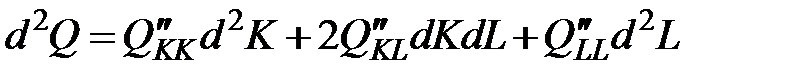 преобразуется к виду:
преобразуется к виду: 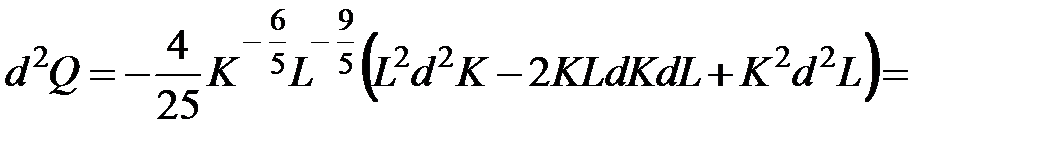
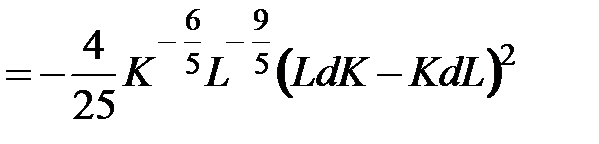 , т.е. является неположительно определенной квадратичной формой, а, значит, функция Кобба-Дугласа является вогнутой функцией.
, т.е. является неположительно определенной квадратичной формой, а, значит, функция Кобба-Дугласа является вогнутой функцией.
Применяем теорему Куна-Таккера. Составим функцию Лагранжа
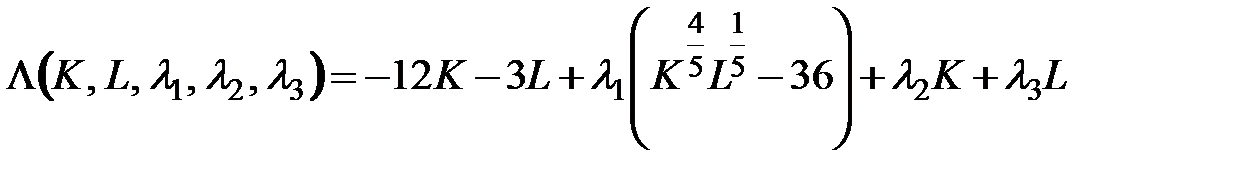 .
.
Тогда имеем систему условий Куна-Таккера
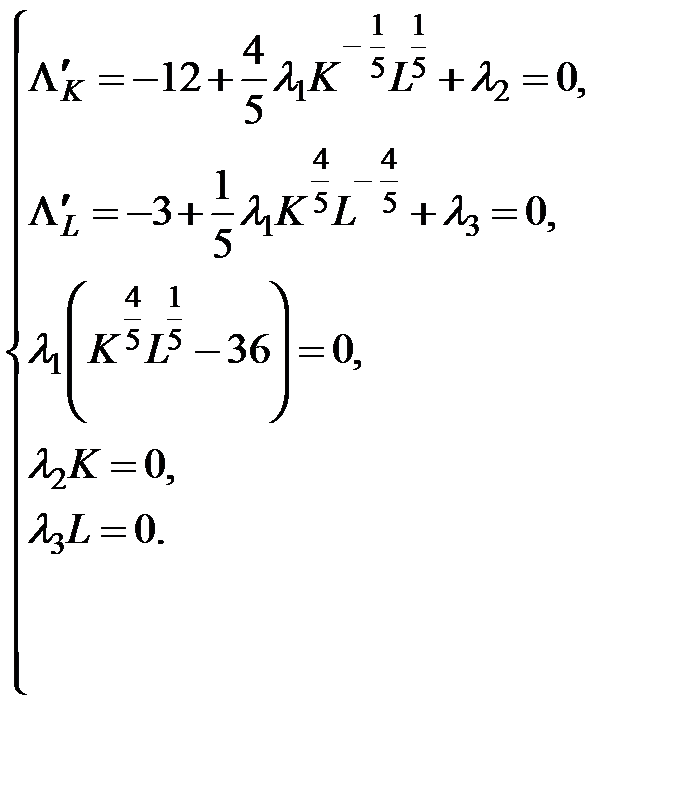
Так как 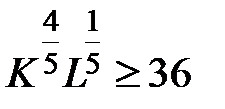 , то
, то 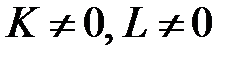 , а поэтому
, а поэтому 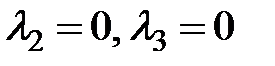 и
и 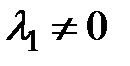 . Система сводится к:
. Система сводится к:
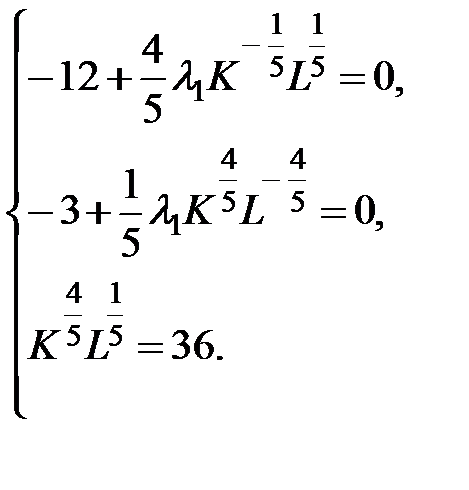 т.е.
т.е. 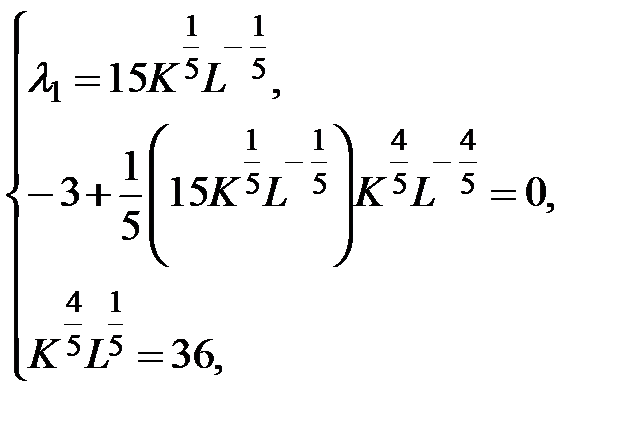

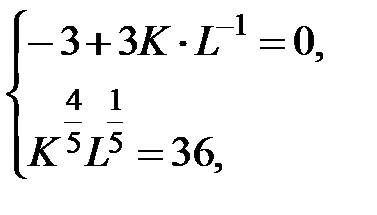

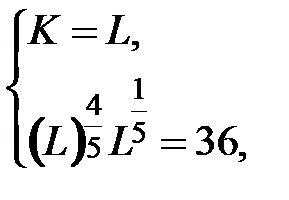 ,
, 

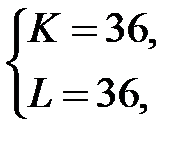
Тогда 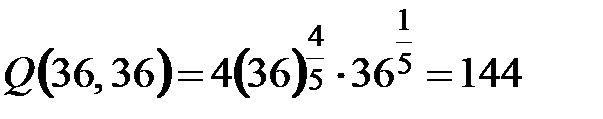 .
.
 2015-05-18
2015-05-18 212
212








