2015-05-18
199
Составим математическую модель задачи. Пусть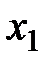 
, 
, 
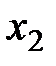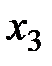– количество изготавливаемых автомобилей первой, второй и третьей моделей соответственно. Тогда в первом цехе на их производство будет потрачено (
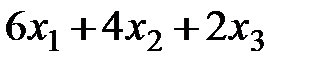) человеко-дней. По условию это количество не должно превосходить мощности первого цеха., т.е. 
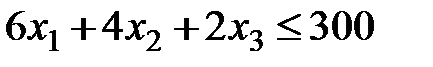. Аналогично получаются ограничения для второго и третьего цехов. Количество изготавливаемых автомобилей 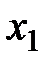, , 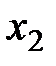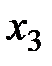физически является неотрицательными величинами. Получим систему ограничений:
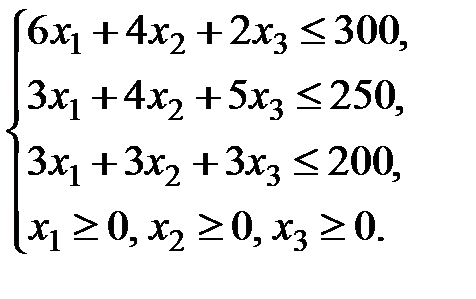
Целевая функция задачи представляет собой общую прибыль от продажи автомобилей всех моделей:
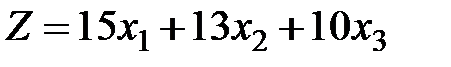(тыс. долл.),
для которой требуется найти максимальное значение в поставленных ограничениях.
Таким образом, математическая модель следующая:
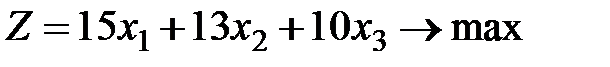
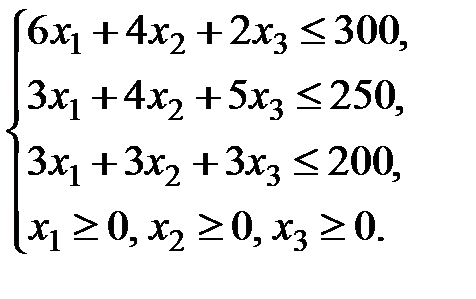
Для решения задачи симплекс–методом приведем задачу к каноническому виду, введя дополнительные балансовые переменные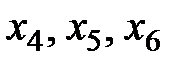 
.Неравенства преобразуются в уравнения путем добавления указанных переменных по одной в каждое неравенство. Переменные 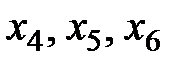также неотрицательны. Введем балансовые переменные в целевую функцию с коэффициентами, равными 0. Тогда каноническая форма задачи следующая:
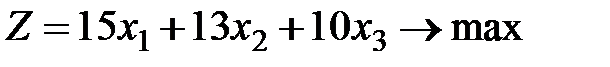
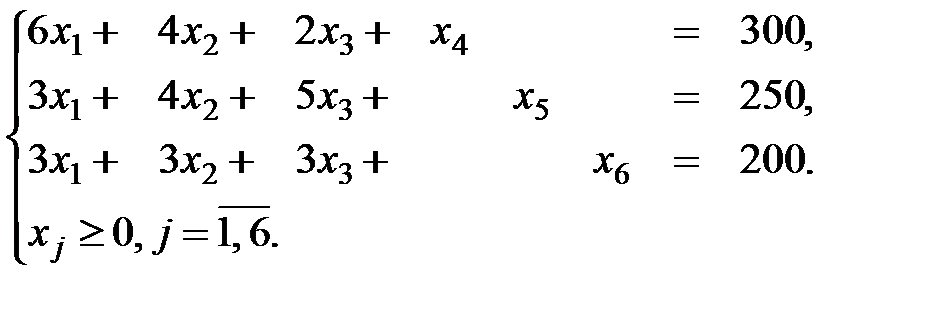
Решаем задачу симплекс-методом. В качестве базисных переменных выбираем балансовые переменные 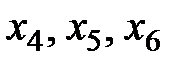, каждая из которых входит только в одно уравнение системы и поэтому матрица коэффициентов при них будет единичной, и, стало быть, невырожденной. Остальные переменные (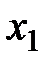, , 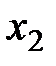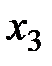) будут свободными. Подставив в последнюю систему 
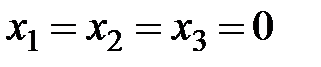, легко получаем значения базисных переменных:
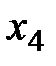= 300; 
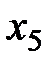= 250; 
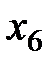= 200.
Тем самым найден исходный опорный план, который в векторном виде запишется:
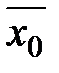= (0; 0; 0; 300; 250; 200).
Подставив компоненты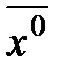 
в целевую функцию, получим её значение для этого плана:
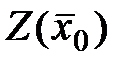= 0.
Теперь составим первоначальную симплексную таблицу (табл.1):
Таблица 1
| Базис |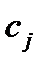 
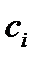
| План |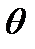 
| ||||||
| 
| 
| 
| 
| 
| ||||
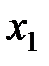
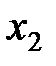
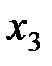
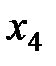
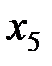
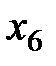
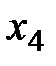
| 300/6=50 | ||||||||
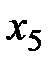
| 250/3=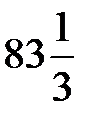 
| ||||||||
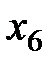
| 200/3=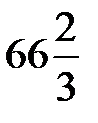 
| ||||||||
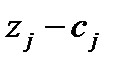
| -15 | -13 | -10 |
Переменная, которая войдет в число базисных – это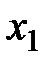 
, так как ей в индексной строке соответствует наименьшее отрицательное число -15. Переменная, “покидающая” число базисных – это 
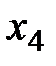, так как ей соответствует минимальное симплексное отношение 
.
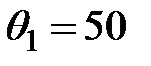Пересчитаем таблицу. Заполнение новой таблицы (табл. 2) начинаем с разрешающей строки – строки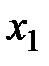 
. Элементы разрешающей строки прежней таблицы делим на разрешающий элемент, который равен 6. Для заполнения второй строки табл. 2 умножим каждый элемент первой строки таблицы 2 на (-3) и прибавим к соответствующему элементу строки 2 таблицы 1. Для заполнения третьей строки табл. 2 умножим каждый элемент первой строки таблицы 2 на (-3) и прибавим к соответствующему элементу строки 3 таблицы 1. Получаем:
Таблица 2
| Базис |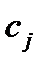
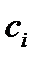
| План |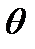
| ||||||
|
|
|
|
|
|
| ||||
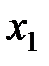
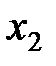
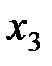
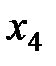
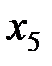
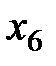
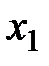
| 2/3 | 1/3 | 1/6 |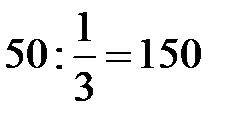 
| |||||
|
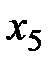
| -1/2 | 100/4=25 | |||||||
|
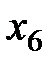
| -1/2 | 50/2=25 | |||||||
|
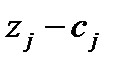
| -3 | -5 | 5/2 |
Произошел переход к новым базисным переменным: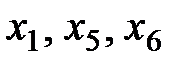 
. При этом переменные 
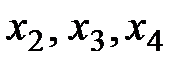являются свободными, и в новом опорном плане их значения равны нулю. Значения остальных переменных получаем из нового столбца 
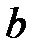свободных членов (находятся напротив единиц базисных переменных):
х1 = 50; х 5 = 100; х 6 = 50.
Запишем опорный план в векторной форме:
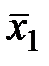= (50; 0; 0; 0; 100; 50).
Этому плану соответствует значение целевой функции, равное 750.
Переменная, которая войдет в число базисных – это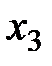 
, так как ей в индексной строке соответствует наименьшее отрицательное число -5. Переменная, “покидающая” число базисных – это 
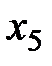, так как ей соответствует минимальное симплексное отношение 
.
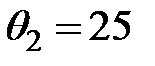Далее по такой же схеме пересчитываем симплексную таблицу 2 первой итерации и получаем табл. 3:
Таблица 3
| Базис |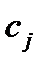
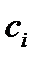
| План |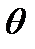
| ||||||
|
|
|
|
|
|
| ||||
|
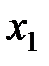
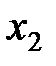
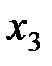
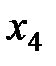
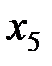
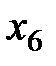
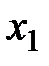
| 125/3 | 1/2 | 5/24 | -1/12 |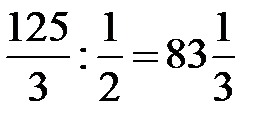 
| ||||
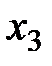
| 1/2 | -1/8 | 1/4 |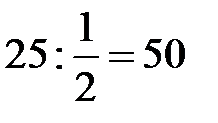 
| |||||
|
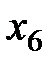
| -1/4 | -1/2 |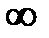 
| ||||||
|
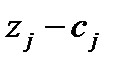
| -1/2 | 15/8 | 5/4 |
Аналогично определяем новый опорный план:
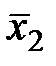= (125/3; 0; 25; 0; 0; 0).
Ему соответствует значение целевой функции, равное 875.
Переменная, которая войдет в число базисных – это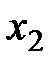 
, так как ей в индексной строке соответствует наименьшее отрицательное число -1/2. Переменная, “покидающая” число базисных – это 
, так как ей соответствует минимальное симплексное отношение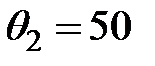 
.
Далее по такой же схеме пересчитываем симплексную таблицу 3 и получаем табл. 4:
Таблица 4
| Базис |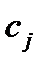
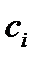
| План |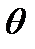
| ||||||
|
|
|
|
|
|
| ||||
|
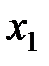
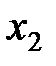
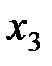
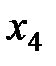
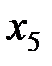
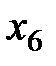
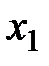
| 50/3 | -1 | 1/3 | -1/3 | |||||
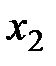
| -1/4 | 1/2 | |||||||
|
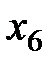
| -1/4 | -1/2 | |||||||
|
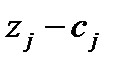
| 7/4 | 3/2 |
Аналогично определяем новый опорный план:
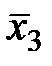= (50/3; 50; 0; 0; 0; 0).
Ему соответствует значение целевой функции, равное 900.
Поскольку в индексной строке уже нет отрицательных элементов, план является оптимальным:
; 
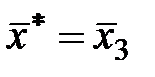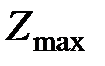= 900.
Итак, задача линейного программирования решена. Возвращаясь к содержательной постановке задачи, можно сказать, что производственная программа, включающая изготовление 50/3 единиц автомобилей первой модели и 50 автомобилей второй модели в декаду, является оптимальной. При этом будет достигнута максимальная стоимость готовой продукции в размере 900 тыс. долл.
Соответственно в месяц необходимо производить 50 единиц автомобилей первой модели и 150 единиц автомобилей второй модели. Максимальная стоимость составит 2700 тыс. долл.
