Составим транспортную таблицу:
Таблица 1
Проверим сбалансированность модели: 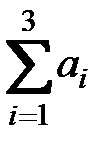 = 260+60+130=450,
= 260+60+130=450, 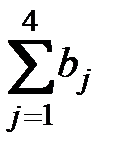 = 90+190+40+130 = 450. Имеем, что
= 90+190+40+130 = 450. Имеем, что 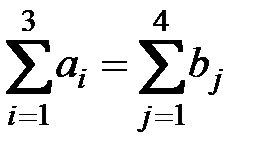 , то есть балансовое равенство выполняется.
, то есть балансовое равенство выполняется.
Отыскание начального решения методом минимального элемента (табл. 2).
Выбираем клетку с наименьшей стоимостью перевозки (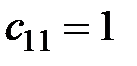 ), объем поставки продукции в этой клетке равен
), объем поставки продукции в этой клетке равен 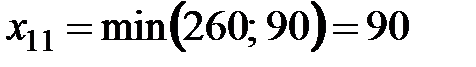 . Тогда запас в первой строке:
. Тогда запас в первой строке: 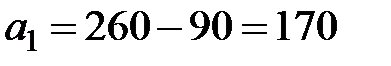 тонн, а первый столбец транспортной таблицы выводим из рассмотрения. Далее
тонн, а первый столбец транспортной таблицы выводим из рассмотрения. Далее 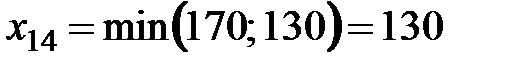 , при этом потребность первого потребителя полностью удовлетворяется (т.е. четвертый столбец транспортной таблицы выходит из рассмотрения), а запас в первой строке еще уменьшается:
, при этом потребность первого потребителя полностью удовлетворяется (т.е. четвертый столбец транспортной таблицы выходит из рассмотрения), а запас в первой строке еще уменьшается: 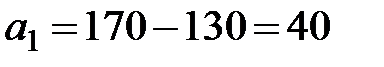 . Далее
. Далее 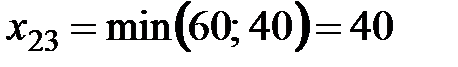 ,
, 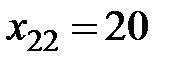 ,
, 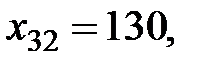
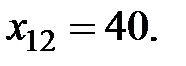 Получено допустимое начальное решение (опорный план) (см. таблицу 2), удовлетворены нужды всех потребителей и использованы все запасы складов.
Получено допустимое начальное решение (опорный план) (см. таблицу 2), удовлетворены нужды всех потребителей и использованы все запасы складов.
Таблица 2
Проверим этот план на оптимальность. Для этого по занятым объемами перевозок клеткам составим систему уравнений вида
|
|
|
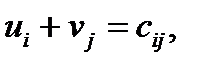 где
где 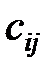 – стоимость перевозки одной единицы груза из пункта – стоимость перевозки одной единицы груза из пункта 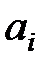 в пункт в пункт 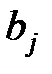 , , 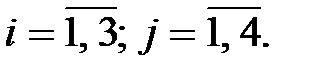
| (1) |
 , ,  – потенциалы. – потенциалы.
|
По формуле (1) имеем:
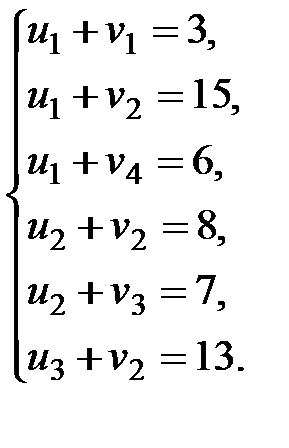
Неизвестные потенциалы 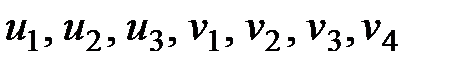 находим из этой системы уравнений, полагая
находим из этой системы уравнений, полагая 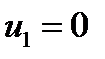 . Тогда из первого уравнения
. Тогда из первого уравнения 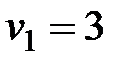 , из второго
, из второго 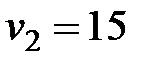 , из третьего
, из третьего 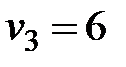 . Далее из четвертого
. Далее из четвертого 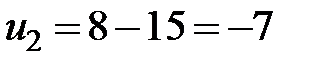 , затем из пятого уравнения
, затем из пятого уравнения 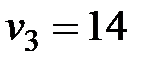 , и, наконец, из последнего
, и, наконец, из последнего 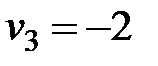 .
.
Перепишем матрицу перевозок, добавив справа столбец с потенциалами 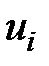 , а внизу строку с потенциалами
, а внизу строку с потенциалами 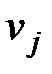 (табл.3).
(табл.3).
Таблица 3
| |||||
| 0 | |||||
| 8 + | 7 - | -7 | |||
| 13 - | 9 + | -2 | |||
| 3 | 15 | 14 | 6 |
Посчитаем оценки свободных клеток по формуле:
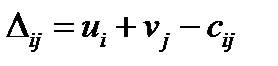 (2):
(2):
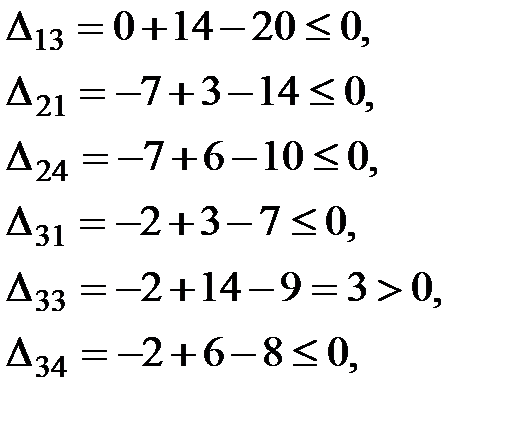
План не оптимальный, так как есть положительная оценка – это оценка 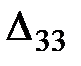 . Поэтому ставим в клетке (3, 3) знак «+» и строим цикл (табл. 3).
. Поэтому ставим в клетке (3, 3) знак «+» и строим цикл (табл. 3).
Вершинам цикла поочередно присваиваем знаки «-» и «+». Из объемов груза, стоящих в минусовых клетках выбираем наименьший 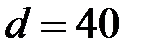 .
.
Строим новый опорный план. В таблице 4 прибавляют 40 к объемам груза в «плюсовых» клетках и вычитают 40 из объемов «минусовых» клеток.
Таблица 4
| |||||
| 0 | |||||
| -7 | |||||
| -2 | |||||
| 3 | 15 | 11 | 6 |
По формуле (1) имеем систему для нахождения потенциалов:
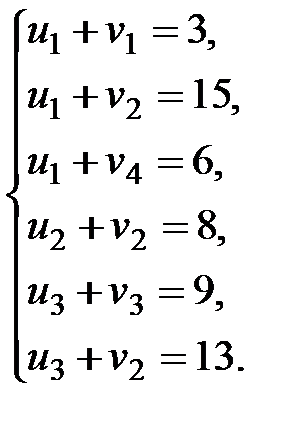
Найденные из системы потенциалы, записываем в таблицу 4.
|
|
|
Посчитаем оценки свободных клеток:
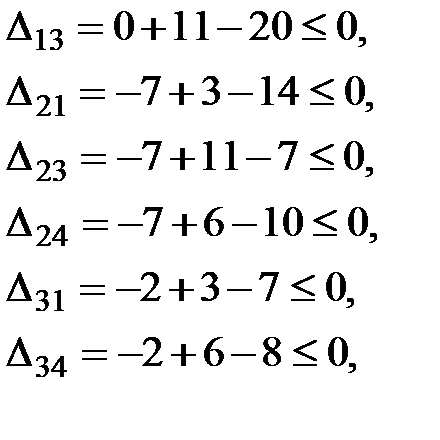
Все оценки свободных клеток не положительны, то есть полученный план перевозок является оптимальным:
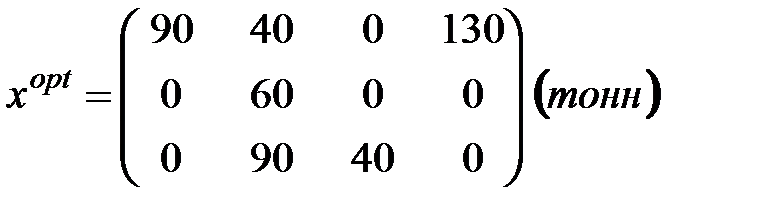
Стоимость перевозки 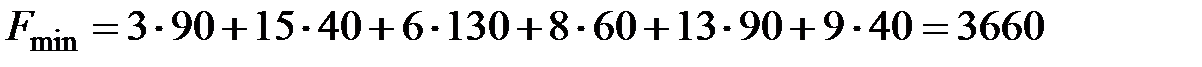 усл. ед.
усл. ед.
 2015-05-18
2015-05-18 215
215







