1.Вычислить максимальное (статическое) значение силы инерции возникающую из-за неуравновешенности ротора по формуле 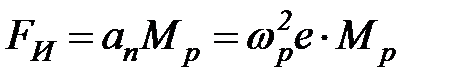 , где
, где 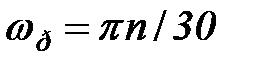 - угловая скорость ротора в [рад/с],
- угловая скорость ротора в [рад/с], 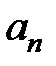 - центробежное ускорение. Во всех схемах можно учитывать только вертикальную составляющую силы инерции, так как горизонтальная составляющая не вызывает изгиба в конструкции (проверить самостоятельно). Горизонтальная составляющая вызывает только деформацию растяжения-сжатия, напряжения и перемещения при этом значительно меньше чем при изгибе.
- центробежное ускорение. Во всех схемах можно учитывать только вертикальную составляющую силы инерции, так как горизонтальная составляющая не вызывает изгиба в конструкции (проверить самостоятельно). Горизонтальная составляющая вызывает только деформацию растяжения-сжатия, напряжения и перемещения при этом значительно меньше чем при изгибе.
2.Определить жесткость конструкции в точке крепления двигателя по вертикали по формуле 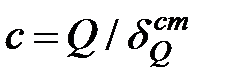 , где
, где 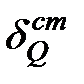 - прогиб конструкции в указанной точке от статического действия веса двигателя
- прогиб конструкции в указанной точке от статического действия веса двигателя 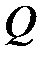 .
.
3.Определить частоту собственных колебаний 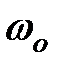 конструкции по формуле
конструкции по формуле 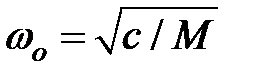 , как для системы с одной степенью свободы. Рассчитать коэффициент динамичности при вынужденных колебаниях
, как для системы с одной степенью свободы. Рассчитать коэффициент динамичности при вынужденных колебаниях 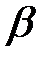 по формуле
по формуле 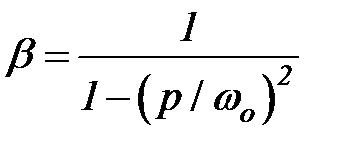 , частота изменения вынуждающей силы при этом
, частота изменения вынуждающей силы при этом 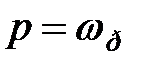 . Проверить условие динамической устойчивости конструкции, которое заключается в том, чтобы при установившемся режиме работы двигателя конструкция была далека от резонанса:
. Проверить условие динамической устойчивости конструкции, которое заключается в том, чтобы при установившемся режиме работы двигателя конструкция была далека от резонанса: 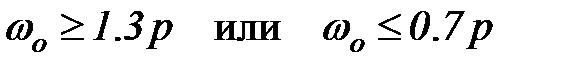 . Если это условие изначально не выполняется, то обеспечить его либо поменяв жесткость системы (взяв другой номер профиля), либо изменив величину сосредоточенной массы (т.е прикрепив к конструкции в месте установки двигателя дополнительную массу).
. Если это условие изначально не выполняется, то обеспечить его либо поменяв жесткость системы (взяв другой номер профиля), либо изменив величину сосредоточенной массы (т.е прикрепив к конструкции в месте установки двигателя дополнительную массу).
4.Определить максимальные нормальные напряжения изгиба в конструкции при установившихся вынужденных колебаниях, заменив двигатель максимальной вертикальной силой 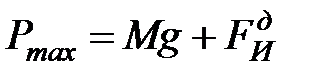 .
.
5. Определить максимальные нормальные напряжения изгиба в конструкции при монтаже двигателя, вычислив коэффициент динамичности 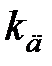 при падении двигателя по формуле
при падении двигателя по формуле 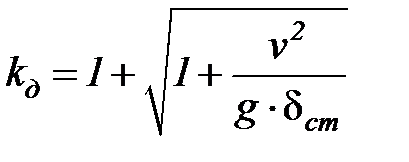 , где
, где 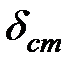 - статический вертикальный прогиб от веса груза. Динамическая вертикальная сила при падении двигателя
- статический вертикальный прогиб от веса груза. Динамическая вертикальная сила при падении двигателя 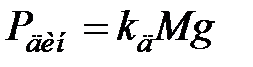 .
.
 2015-05-18
2015-05-18 435
435








