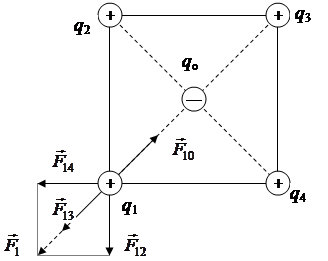
 Задача 1. В центре квадрата, в каждой вершине которого находится заряд равный 2,4 нКл, помещен отрицательный заряд q o. Найти этот заряд, если на каждый заряд в вершине действует результирующая сила, равная 0,4 мН. Сторона квадрата 1 см.
Задача 1. В центре квадрата, в каждой вершине которого находится заряд равный 2,4 нКл, помещен отрицательный заряд q o. Найти этот заряд, если на каждый заряд в вершине действует результирующая сила, равная 0,4 мН. Сторона квадрата 1 см.
| Дано: а = 1см =10—2м. q 1 = q 2 = q 3 = q 4 = 2,4 нКл = 2,4 . 10—9Кл F =0,4мН=0,4 . 10—3Н | Решение. |
| q o —? |
Результирующая сила F, действующая на каждый из зарядов, находящихся в
вершинах квадрата, равна 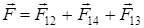
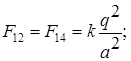
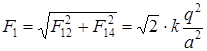 ,
,
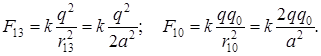
Отсюда:
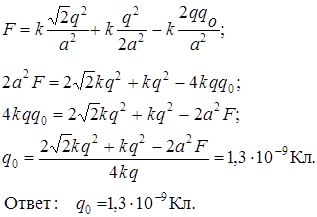
Задача 2. Два заряда q 1 = q и q 2 = -4 q находятся на расстоянии r = 10 см друг от друга. Третий заряд q 3 может перемещаться только вдоль прямой, проходящей через заряды. Определите положение заряда q 3 , при котором он будет находиться в равновесии.
| Дано: q 1 = q; q 2 = -4 q; r = 10см | Решение. Заряд будет находиться в равновесии, если 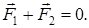 Из рисунка видно, что это условие может быть выполнено лишь на рис. (а). Из рисунка видно, что это условие может быть выполнено лишь на рис. (а). |
| х —? |
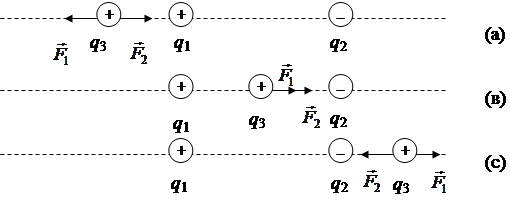 |
Расстояние от меньшего по модулю заряда q 1 до q 3 на рис. (а) обозначим через х. Тогда расстояние от заряда q 2 до заряда q 3 будет равно (r + x).
Выражая в условии равновесия силы F 1 и F 2 в соответствии с законом Кулона, получим
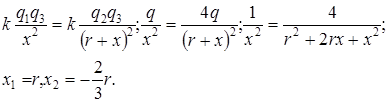
Физическому условию задачи удовлетворяет корень х 1 = r.
Ответ: х = r.
Задача 3. Электрическое поле создано двумя точечными зарядами q 1=30 нКл и q 2=-10 нКл Расстояние d между зарядами равно 20 см. Определите напряженность электрического поля в точке, находящейся на расстоянии r 1=15 см от первого и на расстоянии r 2=10 см от второго заряда.
| Дано: q 1 = 30 нКл = 3 . 10-8 Кл; q 2 = -10 нКл = -10 . 10-8 Кл; d = 20 см = 0,2м; r 1 = 15 см = 0,15 м; r 2 = 10 см = 0,1 м; | Решение. 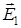 α α 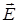 α α 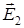 q 1 d q 2 q 1 d q 2 |
| Е —? |
Согласно принципа суперпозиции:
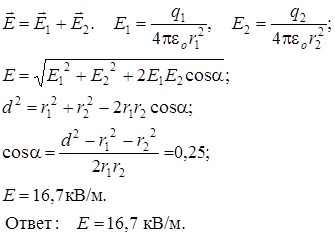
Задача 4. Заряд q =1,5 . 10—8 Кл равномерно распределен по кольцу радиуса R =0,2м. Найдите напряженность электрического поля в точке, находящейся на оси кольца на расстоянии h =0,15 м от его центра.
| Дано: q =1,510-9 Кл R =0,2 м h =0,15 м | Решение. Заряд q не является точечным, поэтому кольцо разбивается на элементарные части, заряд dq, которые можно считать точечными. |
| E —? |
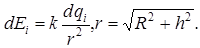
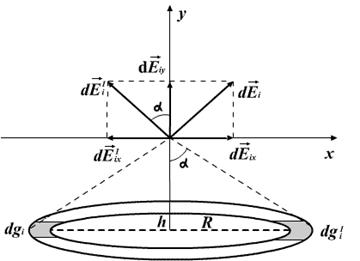 |
Согласно принципа суперпозиции: 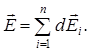 Вектор d
Вектор d 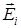 можно разложить на составляющие dEix и dEiy . Тогда
можно разложить на составляющие dEix и dEiy . Тогда 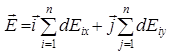 ,
, 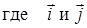 — единичные вектора (орты).
— единичные вектора (орты).
Очевидно, что 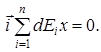 Таким образом
Таким образом 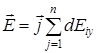 .
.
dEiy = dEi ·cosα, 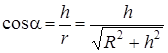
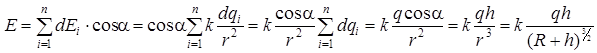
Ответ: E =1,3·103 (В/м).
Задача 5. Заряд точечный q о = —2×10—10 Кл расположен на продолжении оси диполя, электрический момент которого р е = —1,5×10—10 Кл×м, на расстоянии r =10 см от его центра (ближе к положительному заряду диполя). Какую работу надо совершить, чтобы перенести этот заряд в симметрично расположенную точку по другую сторону диполя.
 Дано: q о = -2. 10-10 Кл р е = -1,5 . 10-10 Кл. м, r = 10 см Дано: q о = -2. 10-10 Кл р е = -1,5 . 10-10 Кл. м, r = 10 см | Решение. Работа А *, совершаемая внешними силами при перемещении заряда в электрическом поле, равна работе |
| А *—? | сил поля, взятой с обратным знаком. |
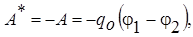
где j1 и j2 - потенциалы точек В и С.
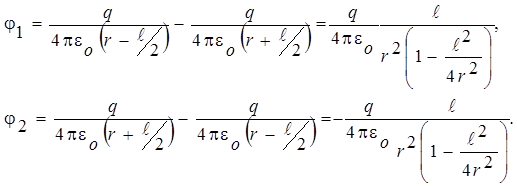
Если учесть, что 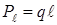 и при r >>
и при r >> 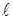 выражениями
выражениями 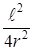 в знаменателе можно пренебречь, то формулы для j1 и j2 принимают вид:
в знаменателе можно пренебречь, то формулы для j1 и j2 принимают вид:
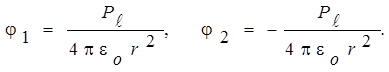
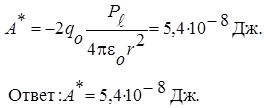
Задача 6. Тонкий стержень длиной 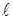 =10 см равномерно заряжен зарядом q = -3×10-9 Кл. Определите напряженность и потенциал поля в точке С, лежащей на оси стержня. На расстоянии x 0 от середины стержня до этой точки.
=10 см равномерно заряжен зарядом q = -3×10-9 Кл. Определите напряженность и потенциал поля в точке С, лежащей на оси стержня. На расстоянии x 0 от середины стержня до этой точки.
Дано: x o= 20 см q = -3. 10—9 Кл 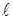 = 10 см = 10 см | Решение. Заряд не является точечным, поэтому стержень разбивается на элементарные отрезки dx, заряд dq на которых можно считать точечным. |
| E c —? j c —? | 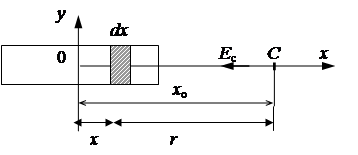 |
Потенциал поля, создаваемый в точке С зарядом dq, равен
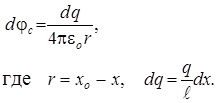
Потенциал поля, создаваемый в точке С всем стержнем, находится интегрированием
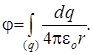
Таким образом,
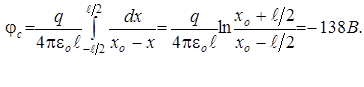
Напряженность поля вдоль оси OX равна
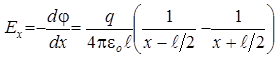 .
.
Отсюда 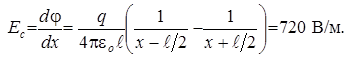
Ответ: φc= -138 В; E c= 720 В/м.
Задача 7. В плоский конденсатор влетает электрон со скоростью V = 2×107 м/c, направленной параллельно пластинам конденсатора. На какое расстояние от своего первоначального направления сместится электрон за время пролета конденсатора? Расстояние между пластинами d = 2 см, длина пластин конденсатора 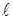 =5 см, разность потенциалов между пластинами U = 200 В.
=5 см, разность потенциалов между пластинами U = 200 В.
Дано: V о = 2. 10-7 м/с d = 2 см = 2. 10-2 м 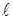 = 5 см U = 200 В m = 9,1. 10-31 кг e = 1,6. 10-19 Кл = 5 см U = 200 В m = 9,1. 10-31 кг e = 1,6. 10-19 Кл | Решение. 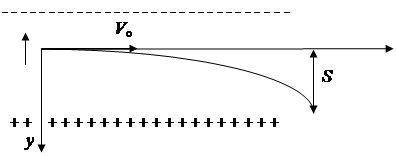 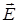 |
| S —? |
Движение электрона вдоль оси ОХ является равномерным, вдоль оси ОУ - равноускоренным.
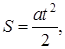
где a – ускорение, приобретаемое электроном под действием силы F = eE. 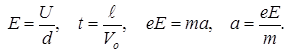
Отсюда 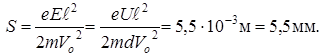
Ответ: S = 5,5 мм.
Задача 8. Плоский воздушный конденсатор с площадью S пластины, равной 500 см2, подключен к источнику тока, ЭДС которого равен 300 В. Определить работу А внешних сил по раздвижению пластин от расстояния d 1 = 1 см до d 3 = 3 см в двух случаях: 1) пластины перед раздвижением отключаются от источника тока; 2) пластины в процессе раздвижения остаются подключенными к нему.
| Дано: S = 500 см2= =5. 10—2 м2 U = 300 B d 1 = 1 см d 3 = 3 см | Решение. Работа внешних сил равна изменению энергии конденсатора: А = W 2 — W 1. 1) Заряд на обкладках конденсатора остается постоянным, так как конденсатор отключен от источника |
| А —? | q = C 1 Dφ = const, где Dφ равна ЭДС источника U. |
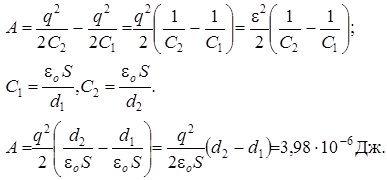
2) Пластины остаются подключенными к источнику тока, и система не является изолированной. Заряд с пластин при их раздвижении перемещается к клеммам батареи. В этом случае остается неизменной разность потенциалов между пластинами Dφ = U, поэтому энергию конденсатора удобно представить в виде: 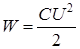 ,
,
тогда 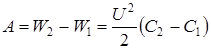 . Таким образом
. Таким образом
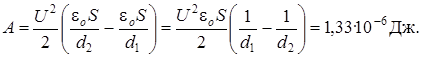
Ответ: 1) А = 3,98·10-6 Дж; 2) A = 1,33·10-6 Дж.
Задача 9. Расстояние d между пластинами плоского конденсатора равно 2 мм, разность потенциалов U = 1,8 кВ. Диэлектрик - стекло. Определите диэлектрическую восприимчивость χ стекла и поверхностную плотность s ¢ связанных зарядов на поверхности стекла.
| Дано: d = 2 мм U = 1,8 кВ e = 7,0 | Решение. e = 1 + χ, χ = e - 1 = 6. s ¢ = Р, где Р — поляризованность диэлектрика. Р = χ eо Е, где Е = U / d — напряженность поля в |
| s ¢—? | диэлектрике. |
Отсюда: s ¢ = χ eо (U / d) = 47,7 . 10—6 Кл/м2.
Ответ: χ = 6, s ¢ = 47,7 . 10—6 Кл/м2.
Задача 10. Плоская квадратная пластина со стороной a =0,1 м находится на некотором расстоянии от бесконечной, равномерно заряженной плоскости (s=1 мкКл/м2). Плоскость пластины составляет угол b=30о с линиями поля. Найти поток Ф вектора электрической напряженности через эту пластину.
| Дано: a = 0.1 м s=1 мкКл/м2 b = 30о | Решение.  +s +s  a a  b b |
| Ф —? |
Заряженная плоскость создает однородное электрическое поле с напряженностью 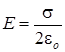 . Таким образом Ф = E·S· cosa.
. Таким образом Ф = E·S· cosa.
Учитывая, что 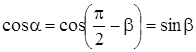 , окончательно получаем
, окончательно получаем 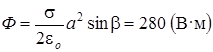
Ответ: Ф=280 В·м.
Задача 11. В центре сферы, радиусом R =20 см, находится точечный заряд q =10-2 мкКл. Определить поток вектора напряженности через часть сферической поверхности площадью S =20 см2.
| Дано: R = 20см = 0.2 м q = 10-2 мкКл S = 20см2 = 20·10-4 м2 | 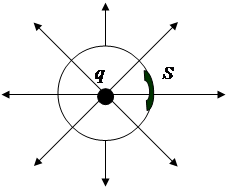 Решение. Решение. |
| Ф —? |
Поток Ф R через всю сферическую поверхность можно определить по теореме Остроградского-Гаусса: 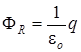 .
.
Искомая часть этого потока, проходящая через S,определяется соотношением 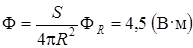 .
.
Ответ: Ф=4,5 В·м.
 2015-05-18
2015-05-18 5854
5854
