Напряженность поля плоского конденсатора (вывод). Удельная сила взаимодействия между двумя бесконечными равномерно заряженными плоскостями

Поле плоского конденсатора можно рассматривать как совокупность полей двух бесконечных разноименно заряженных плоскостей (рис. 2, а и б). Напряженность поля (рис. 2, в) можно найти по принципу суперпозиции:

E ⃗ = E ⃗ 1+ E ⃗ 2,

где E 1= E 2= σ 2 ε 0⋅ ε = q 2 ε 0⋅ ε ⋅ S — напряженности электрических полей каждой из обкладок конденсатора, σ — поверхностная плотность заряда на обкладках конденсатора. Тогда в проекциях на ось 0Х: справа и слева от пластин — E х=0; между пластин — E =2 E 1= qε 0⋅ ε ⋅ S.

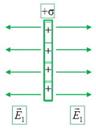
Электроемкость плоского конденсатора C = qU, где U = E ⋅ d, d — расстояние между пластин. Следовательно, C = qE ⋅ d = qd ⋅1 E = qd ⋅ ε 0⋅ ε ⋅ Sq = ε 0⋅ ε ⋅ Sd..

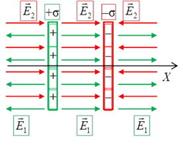
Поле двух параллельных бесконечно больших плоскостей, заряженных разноименно с одинаковой по величине постоянной поверхностной плотностью 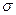можно рассматривать как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. В области между плоскостями (рис.2.13) складываемые поля имеют одинаковое направление, так что результирующая напряженность равна

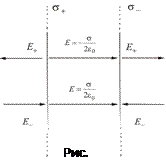
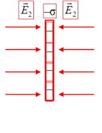
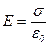Вне объема, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулю E=0. Таким образом, поле сосредоточено между плоскостями. Напряженность поля во всех точках этой области одинакова по величине и по направлению. Поле, обладающее такими свойствами, называется однородным. Линии напряженности однородного поля представляют собой совокупность параллельных равноотстоящих прямых.

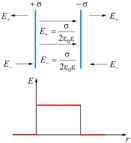
Полученный результат приблизительно справедлив и в случае плоскостей конечных размеров, если расстояние между плоскостями значительно меньше их линейных размеров (плоский конденсатор). В этом случае заметные отклонения поля от однородности напряженности наблюдаются только вблизи краев пластин (рис. 2.14).

Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ.

Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей. Тогда внутри плоскостей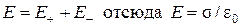

Вне плоскостей напряженность поля .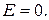

Распределение напряженности электростатического поля между пластинами конденсатора показано на рисунке.

Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин): 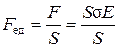, т.е. .

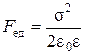Механические силы, действующие между заряженными телами, называют пондермоторными. Тогда сила притяжения между пластинами конденсатора: 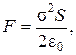где S – площадь о,кладок конденсатора. Т.к. 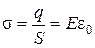, то 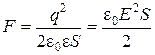. Это формула для расчета пондермоторной силы.