Определение. Случайная величина называется дискретной, или дискретного типа (сокращенно СВДТ), если множество ее возможных значений конечно или счетно.
Простейшей формой закона распределения СВДТ с конечным множеством значений является ряд распределения, который задается аналитически или при помощи таблицы.
Пример 2.1.4. Гипергеометрическое распределение – распределение числа белых шаров X в выборке без возвращения объема n из урны, содержащей М белых и 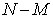 черных шаров:
черных шаров:
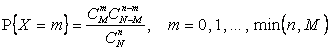 .
.
Пример 2.1.5. Равномерное распределение на множестве 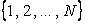 :
:
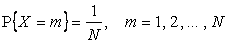 .
.
В ряде распределения, задаваемом при помощи таблицы, в верхней строке расположены по возрастанию все возможные значения 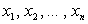 СВДТ X, а в нижней – соответствующие им вероятности
СВДТ X, а в нижней – соответствующие им вероятности 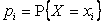 ,
, 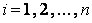 :
:
| X | 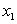
| 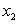
| … | 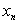
|
| P | 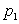
| 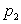
| … | 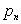
|
Имеет место равенство 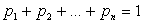 , т.к. события
, т.к. события 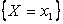 ,
, 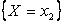 , …,
, …, 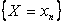 попарно несовместны и образуют полную группу. С помощью этой таблицы можно найти вероятности любых событий:
попарно несовместны и образуют полную группу. С помощью этой таблицы можно найти вероятности любых событий:
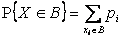 .
.
Пример 2.1.6. Закон распределения СВДТ X задан при помощи таблицы:
| X | ||||
| P | 0,1 | 0,3 | 0,2 | 0,4 |
Найти вероятность события 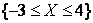 .
.
Решение. 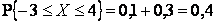 .
.
Ответ: 0,4.
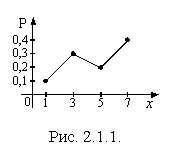 Графическое изображение ряда распределения называется многоугольником распределения. Для случайной величины из примера 2.1.6 многоугольник распределения показан на рис. 2.1.1.
Графическое изображение ряда распределения называется многоугольником распределения. Для случайной величины из примера 2.1.6 многоугольник распределения показан на рис. 2.1.1.
Кроме геометрической интерпретации распределения СВДТ X часто оказывается полезной механическая интерпретация в виде ряда материальных точек 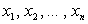 на оси абсцисс, имеющих массы
на оси абсцисс, имеющих массы 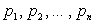 соответственно, причем
соответственно, причем 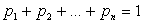 .
.
Зная закон распределения СВДТ X, можно составить функцию распределения 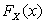 , представляющую собой, согласно определению, функцию накопленных вероятностей:
, представляющую собой, согласно определению, функцию накопленных вероятностей:
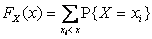 ,
,
где суммирование распространяется на все значения индекса i, для которых 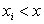 .
.
Из равенства 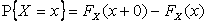 следует, что в точках разрыва функции
следует, что в точках разрыва функции 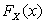 имеет место положительная вероятность
имеет место положительная вероятность 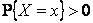 . Так как при каждом натуральном n может быть не более n точек x с вероятностями
. Так как при каждом натуральном n может быть не более n точек x с вероятностями 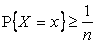 , то у функции
, то у функции 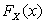 имеется не более счетного числа точек разрыва.
имеется не более счетного числа точек разрыва.
Обозначим 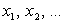 все точки разрыва функции
все точки разрыва функции 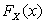 . Если вероятности
. Если вероятности 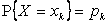 таковы, что
таковы, что 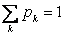 , то это равносильно тому, что случайная величина X имеет дискретное распределение, т.е. является СВДТ.
, то это равносильно тому, что случайная величина X имеет дискретное распределение, т.е. является СВДТ.
Замечание. Для СВДТ X функция распределения 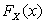 имеет ступенчатый вид, испытывая скачки в точках x, для которых существует положительная вероятность события
имеет ступенчатый вид, испытывая скачки в точках x, для которых существует положительная вероятность события 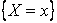 . При этом уточним, что стрелки «ступенек» должны быть, согласно определению
. При этом уточним, что стрелки «ступенек» должны быть, согласно определению 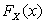 , направлены влево!!!
, направлены влево!!!
Пример 2.1.7. Закон распределения СВДТ задается при помощи таблицы:
| X | –3 | –1 | |||
| P | 0,1 | 0,3 | 0,1 | 0,3 | 0,2 |
Составить функцию распределения и построить ее график. С помощью 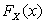 найти вероятности событий
найти вероятности событий  и
и 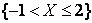 .
.
Решение. По определению 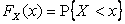 , поэтому:
, поэтому:
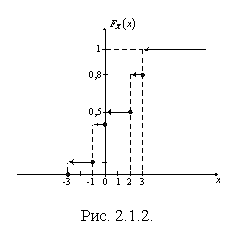
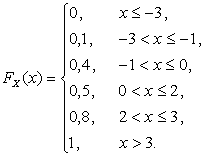
График функции распределения 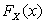 приведен на рис. 2.1.2.
приведен на рис. 2.1.2.
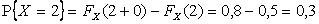 ;
;
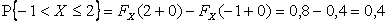 .
.
Ответ: 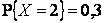 ,
, 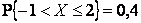 .
.
Введем важное понятие индикатора события.
Определение. Индикатором события 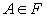 называется СВДТ
называется СВДТ
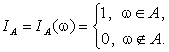
Если р – вероятность события А, то ряд распределения случайной величины 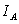 имеет следующий вид:
имеет следующий вид:
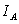
| ||
| P | 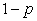
| p |
Многоугольник распределения СВДТ 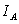 (при
(при 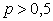 ) построен на рис. 2.1.3 а. Функция распределения СВДТ
) построен на рис. 2.1.3 а. Функция распределения СВДТ 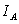 :
:
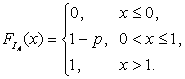
График функции распределения 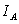 приведен на рис. 2.1.3 б.
приведен на рис. 2.1.3 б.


а б
Рис. 2.1.3.
Пример 2.1.8. Законы распределений СВДТ X и Y заданы при помощи таблиц:
| X | –1 | Y | ||||
| P | 0,5 | 0,5 | P | 0,5 | 0,5 |
Сравнить 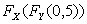 и
и 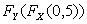 .
.
Решение. Используя ряды распределений, получим:
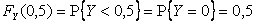 ,
,
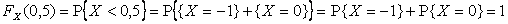 .
.
Тогда
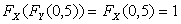 ,
,
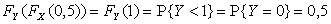 .
.
Значит, 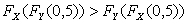 .
.
Ответ: 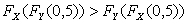 .
.
Пример 2.1.9. В урне 5 белых и 25 черных шаров. Вынули один шар. Случайная величина Х – число вынутых белых шаров. Составить функцию распределения 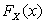 .
.
Решение. Поскольку вынимается только один шар, то возможны два элементарных исхода:
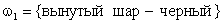 ,
, 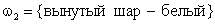 .
.
Поэтому случайная величина Х – число вынутых белых шаров – может принимать только два значения: 0 и 1. При этом 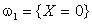 ,
, 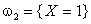 . Ясно, что
. Ясно, что
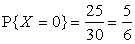 ,
, 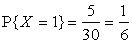 .
.
Можно построить ряд распределения
| X | ||
| P | 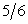
| 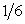
|
Функция распределения СВДТ X:
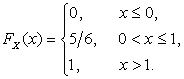
Ответ: 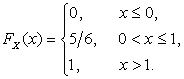
 2015-05-20
2015-05-20 713
713








