Пусть на прямой в точках 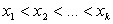 расположены точечные массы
расположены точечные массы 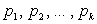 ,
, 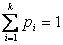 . В этом случае
. В этом случае 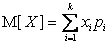 – центр тяжести,
– центр тяжести, 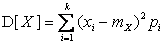 – момент инерции масс
– момент инерции масс 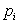 относительно центра тяжести. Таким образом, математическое ожидание характеризует место, вокруг которого группируются массы
относительно центра тяжести. Таким образом, математическое ожидание характеризует место, вокруг которого группируются массы 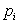 , а дисперсия – степень разбросанности этих масс около математического ожидания.
, а дисперсия – степень разбросанности этих масс около математического ожидания.
В заключение этого пункта вычислим математическое ожидание, дисперсию и среднее квадратическое отклонение 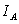 (здесь
(здесь 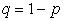 ):
):
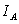 | ||
| P | q | p |
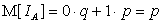 ,
,
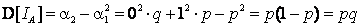 ,
, 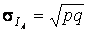 .
.
Пример 2.1.17. Закон распределения случайной величины X имеет вид:
| X | |||
| P | 0,1 | 0,2 | x |
Найти x. Составить функцию распределения. Вычислить: 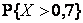 ,
, 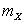 ,
, 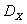 и
и 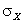 .
.
Решение. Согласно условию нормировки имеем уравнение: 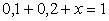 . Отсюда
. Отсюда 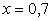 . Далее, воспользовавшись рядом распределения, найдем:
. Далее, воспользовавшись рядом распределения, найдем:
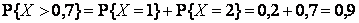 ,
,
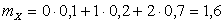 ,
,
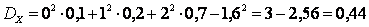 ,
,
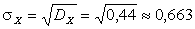 .
.
Ответ: 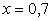 ,
, 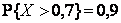 ,
, 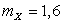 ,
, 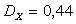 ,
, 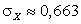 .
.
Пример 2.1.18. Известно, что случайная величина X, принимающая два значения 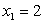 и
и 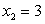 , имеет математическое ожидание, равное 2,2. Построить ряд распределения случайной величины X, найти дисперсию, среднее квадратическое отклонение и составить функцию распределения.
, имеет математическое ожидание, равное 2,2. Построить ряд распределения случайной величины X, найти дисперсию, среднее квадратическое отклонение и составить функцию распределения.
Решение. Пусть 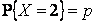 . Тогда, согласно условию нормировки,
. Тогда, согласно условию нормировки, 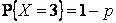 . Используя определение математического ожидания, получим
. Используя определение математического ожидания, получим 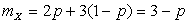 . Имеем уравнение
. Имеем уравнение 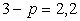 , откуда находим
, откуда находим 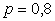 . Ряд распределения имеет вид:
. Ряд распределения имеет вид:
| X | ||
| P | 0,8 | 0,2 |
Теперь вычислим дисперсию и среднее квадратическое отклонение:
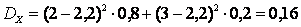 ;
; 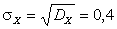 .
.
Согласно определению функция распределения имеет вид
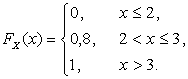
Ответ: 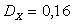 ,
, 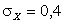 ,
, 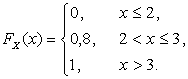
Пример 2.1.19. Возможные значения случайной величины X таковы: 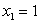 ,
, 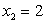 ,
, 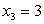 . Известно, что
. Известно, что 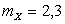 ,
, 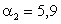 . Найти вероятности, соответствующие возможным значениям X, и записать ряд распределения.
. Найти вероятности, соответствующие возможным значениям X, и записать ряд распределения.
Решение. Ряд распределения, с учетом возможных значений случайной величины X, будет выглядеть следующим образом:
| X | |||
| P | 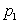 | 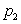 | 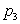 |
Найдем вероятности 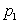 ,
, 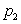 и
и 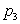 , соответствующие возможным значениям X.
, соответствующие возможным значениям X.
По условию 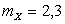 , поэтому имеем первое уравнение, связывающее
, поэтому имеем первое уравнение, связывающее 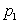 ,
, 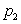 и
и 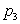 :
: 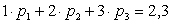 . Аналогично из условия
. Аналогично из условия 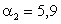 получим второе уравнение:
получим второе уравнение: 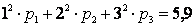 . Третье уравнение возникает из условия нормировки:
. Третье уравнение возникает из условия нормировки: 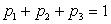 . Итак, имеем систему:
. Итак, имеем систему:
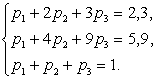
Решением системы, опуская промежуточные выкладки, являются следующие числа: 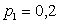 ,
, 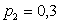 ,
, 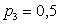 .
.
Ответ: ряд распределения имеет вид
| X | |||
| P | 0,2 | 0,3 | 0,5 |
Пример 2.1.20. Плотность 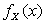 случайной величины X представлена на графике (рис. 2.1.7). Найти константу h. Составить функцию распределения
случайной величины X представлена на графике (рис. 2.1.7). Найти константу h. Составить функцию распределения 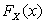 и построить ее график. Найти
и построить ее график. Найти 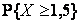 , математическое ожидание и дисперсию случайной величины Х.
, математическое ожидание и дисперсию случайной величины Х.
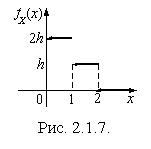 Решение. 1) Найдем константу h из условия нормировки. Имеем уравнение
Решение. 1) Найдем константу h из условия нормировки. Имеем уравнение 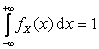 , или, исходя из геометрического смысла интеграла,
, или, исходя из геометрического смысла интеграла, 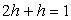 . Отсюда
. Отсюда 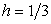 . Таким образом, функция плотности
. Таким образом, функция плотности 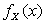 имеет вид:
имеет вид:
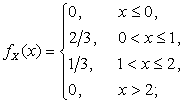
2) По определению 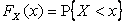 .
.
Пусть 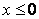 , тогда
, тогда 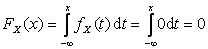 .
.
Пусть 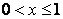 , тогда
, тогда 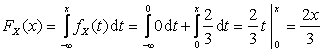 .
.
Пусть 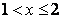 , тогда
, тогда
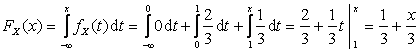 .
.
Пусть 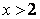 , тогда
, тогда 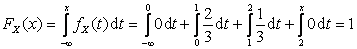 .
.
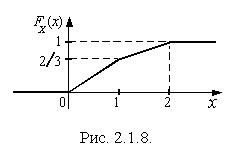 Таким образом, функция распределения
Таким образом, функция распределения 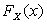 :
:
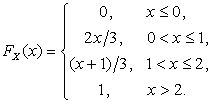
График функции распределения 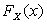 приведен на рис. 2.1.8.
приведен на рис. 2.1.8.
3) 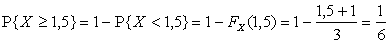 .
.
4) По определению математического ожидания 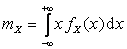 , поэтому:
, поэтому:
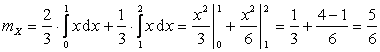 .
.
По определению дисперсии 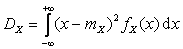 , поэтому:
, поэтому:
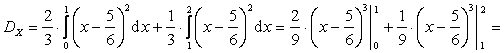
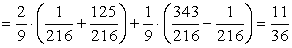 .
.
Ответ: 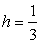 ,
, 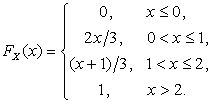 ,
, 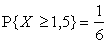 ,
, 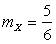 ,
, 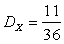 .
.
 2015-05-20
2015-05-20 2132
2132
