Среди числовых характеристик особое значение имеют моменты – начальные и центральные.
Определение. Начальным моментом s-го порядка случайной величины Х называется действительное число 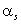 , определяемое по формуле:
, определяемое по формуле:
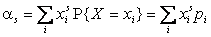 , если X – СВДТ;
, если X – СВДТ;
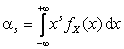 , если X – СВНТ.
, если X – СВНТ.
Замечание. Начальный момент 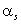 существует, если ряд (соответственно интеграл) в правой части каждой из этих формул сходится абсолютно.
существует, если ряд (соответственно интеграл) в правой части каждой из этих формул сходится абсолютно.
Замечание. Иногда используются абсолютные начальные моменты s-го порядка случайной величины X:
 , если X – СВДТ;
, если X – СВДТ;
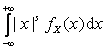 , если X – СВНТ;
, если X – СВНТ;
Определение. Начальный момент первого порядка 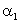 называется математическим ожиданием (средним значением по распределению) случайной величины Х.
называется математическим ожиданием (средним значением по распределению) случайной величины Х.
Математическое ожидание случайной величины X обозначается 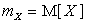 и выражается через ее закон распределения с помощью формулы:
и выражается через ее закон распределения с помощью формулы:
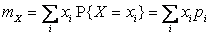 , если X – СВДТ;
, если X – СВДТ;
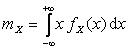 , если X – СВНТ.
, если X – СВНТ.
Математическое ожидание в теории вероятностей относится к типу характеристик положения (см. далее мода, медиана).
Определение. Случайная величина называется центрированной, если ее математическое ожидание равно нулю.
Общепринятым для центрированной случайной величины является обозначение 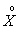 . По определению
. По определению 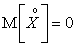 .
.
Пример 2.1.13. Закон распределения случайной величины X имеет вид:
| X | –1 | |||
| P | 0,1 | 0,2 | 0,3 | 0,4 |
Вычислить 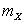 и
и 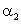 .
.
Решение. По определению 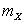 и
и 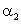 :
:
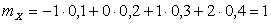 ;
;
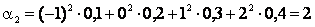 .
.
Ответ: 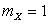 ,
, 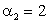 .
.
Пример 2.1.14. Дана функция плотности случайной величины Х:
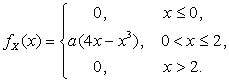
Определить а, затем найти 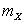 и
и 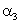 случайной величины Х.
случайной величины Х.
Решение. Константа a ищется из условия нормировки 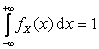 . Имеем уравнение:
. Имеем уравнение:
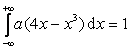 , или
, или 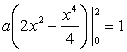 .
.
Отсюда 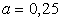 , и функция плотности примет вид:
, и функция плотности примет вид:
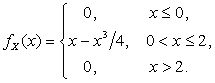
По определению математического ожидания СВНТ X:
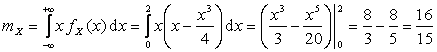 .
.
Найдем теперь начальный момент третьего порядка 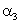 :
:
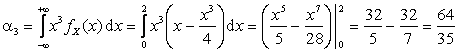 .
.
Ответ: 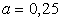 ,
, 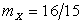 ,
, 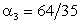 .
.
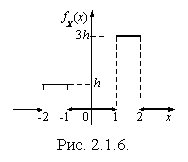 Пример 2.1.15. Плотность
Пример 2.1.15. Плотность 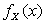 случайной величины X представлена на графике (рис. 2.1.6). Найти константу h и математическое ожидание случайной величины Х.
случайной величины X представлена на графике (рис. 2.1.6). Найти константу h и математическое ожидание случайной величины Х.
Решение. Найдем константу h из условия нормировки. Имеем уравнение 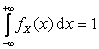 , или, исходя из геометрического смысла интеграла,
, или, исходя из геометрического смысла интеграла, 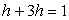 . Отсюда
. Отсюда 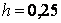 .
.
По определению математического ожидания:
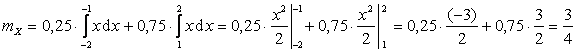 .
.
Ответ: 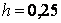 ,
, 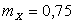 .
.
 2015-05-20
2015-05-20 415
415








