Нормальное распределение имеет широкое распространение в прикладных задачах. Поэтому при изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. С этой целью вводят специальные характеристики, в частности, асимметрию и эксцесс
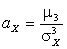 ,
, 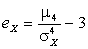 .
.
Для нормального распределения эти характеристики равны нулю. Поэтому если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Наоборот, большие значения 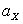 и
и 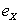 указывают на значительное отклонение от нормального (рис. 2.1.18, 2.1.19).
указывают на значительное отклонение от нормального (рис. 2.1.18, 2.1.19).
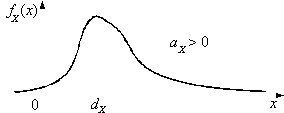 | 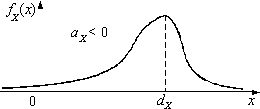 |
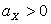 – пологая часть правее моды – пологая часть правее моды | 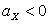 – пологая часть левее моды – пологая часть левее моды |
Рис. 2.1.18.
 |  |
случай 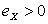 | случай 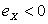 |
Рис. 2.1.19.
Замечание. При исследовании эксцесса надо считать, что нормальное и исследуемое распределения имеют одинаковые математические ожидания и дисперсии.
Пример 2.1.46. Дана функция плотности случайной величины X:
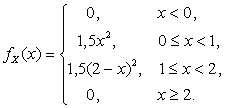
Найти асимметрию и эксцесс случайной величины X.
Решение. Вычислим вначале математическое ожидание и дисперсию случайной величины X (опуская промежуточные выкладки):
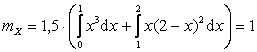 ;
;
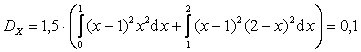 .
.
Отсюда 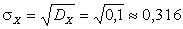 .
.
Также, опуская промежуточные выкладки, вычислим центральные моменты 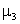 и
и 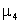 случайной величины X:
случайной величины X:
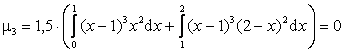 ;
;
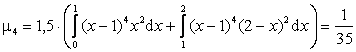 .
.
Заметим, что если построить график плотности 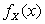 , то можно увидеть, что он имеет вертикальную ось симметрии
, то можно увидеть, что он имеет вертикальную ось симметрии 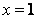 . Поэтому можно было бы, не вычисляя, сразу получить
. Поэтому можно было бы, не вычисляя, сразу получить 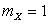 ,
, 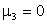 .
.
Теперь находим асимметрию и эксцесс:
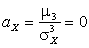 ,
, 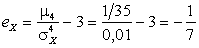 .
.
Ответ: 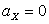 ,
, 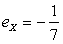 .
.
 2015-05-20
2015-05-20 1041
1041








