2015-05-20
2425
Как уже отмечалось, существуют многочисленные справочники, в которых приведены параметры фильтров, реализующих передаточные функции различных видов. Обычно это НЧ-структуры с частотой среза 1 рад/с. На практике такие фильтры совершенно бесполезны, так как для того или иного конкретного применения необходимы фильтры различных типов с частотами среза от единиц герц до сотен килогерц. Для получения фильтров с требуемыми характеристиками используют процедуру преобразования частоты. Исходный ФНЧ с частотой среза 1 рад/с является НЧ-прототипом. Частотное преобразование заключается в замене комплексной частотной переменной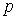 
на новую переменную. С помощью частотных преобразований из нормированного НЧ-прототипа получают фильтры различных типов с требуемой частотой среза. Рассмотрим некоторые из этих преобразований.
Преобразование НЧ–НЧ. Предположим, что нам необходим ФНЧ с частотой среза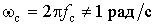 
. Заменим частотную переменную в передаточной функции НЧ-прототипа на новую переменную
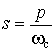. (8.4)
Это равносильно замене катушки, индуктивность которой равна L генри, катушкой индуктивностью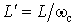 
генри. Конденсатор емкостью С фарад заменяется конденсатором 
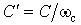фарад. Сопротивления элементов денормированного фильтра на частоте 
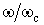будут такими же, как у нормированного фильтра на частоте 
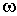. Следовательно, преобразование (8.5) приведет к изменению масштаба по оси частот, и частота среза денормированного фильтра станет равна 
.
Преобразование НЧ–ВЧ. В этом случае преобразование имеет вид:
.
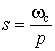Здесь – частота среза фильтра верхних частот. При таком преобразовании передаточная функция ФНЧ-прототипа преобразуется в передаточную функцию ФВЧ с частотой среза . При этом конденсаторы заменяются катушками, индуктивность которых равна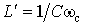 
генри. Аналогично катушки заменяются конденсаторами емкостью 
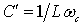фарад.
Преобразование НЧ–ПФ. Это частотное преобразование трансформирует ФНЧ с одной полосой задерживания в полосовой фильтр с двумя полосами задерживания (рис. 8.5).
Преобразование ФНЧ-ПФ выполняется по формуле:
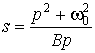. (8.5)
Здесь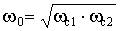 
– центральная частота полосы пропускания; 
, 
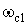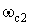– нижняя и верхняя частоты среза; 
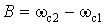– ширина полосы пропускания.
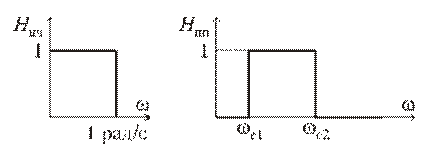Рис. 8.5
Передаточная функция полосового фильтра, получаемая с помощью преобразования (8.5), имеет вдвое больший порядок, чем передаточная функция НЧ-прототипа. Преобразование можно применить как к передаточной функции, так и к схеме исходного ФНЧ. При этом индуктивная катушка преобразуется в последовательное соединение катушки и конденсатора. Действительно, в соответствии с (8.5)
.
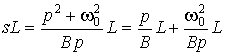Этому равенству соответствует цепь, образованная последовательным соединением катушки индуктивностью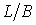 
генри и конденсатора емкостью 
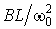фарад. Аналогично конденсатор в ФНЧ-прототипе преобразуется в параллельную цепь, состоящую из конденсатора емкостью 
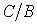фарад и катушки индуктивностью 
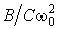генри. В последних соотношениях С – емкость конденсатора в схеме НЧ-прототипа.
Нормирование по сопротивлению. В схемах НЧ-прототипа используются резисторы сопротивлением 1 Ом. Ясно, что на практике требуются фильтры с различными сопротивлениями нагрузки и генератора. При нормировании уровня сопротивления номиналы всех элементов схемы изменяют в определенное число раз. Например, если сопротивление нагрузочного резистора увеличивается в А раз, то индуктивности катушек также необходимо увеличить в А раз, а емкости конденсаторов – уменьшить в А раз. При этом частотные характеристики фильтра не изменятся.
8.4. Активные RC -фильтры
Основной недостаток LC -фильтров, работающих в диапазоне частот менее 50 кГц – большие габариты и вес, обусловленные значительными размерами индуктивных катушек на этих частотах.
Этого недостатка лишены активные RC -фильтры. Такой фильтр содержит резисторы, конденсаторы и активные элементы (как правило, операционные усилители). Активные фильтры широко используют в геофизической, медицинской аппаратуре, устройствах связи. В простых случаях активный фильтр представляет каскадное соединение звеньев второго-первого порядков (рис. 7.6).
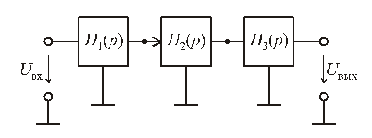
Рис. 8.6
Передаточная функция такого фильтра представляет произведение сомножителей второго порядка:
.
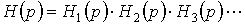Преимущества каскадной реализации заключаются в простоте расчета и настройки фильтра.
Рассмотрим подробнее передаточные функции звеньев второго порядка. В общем случае передаточная функция звена имеет вид
.
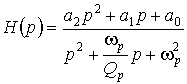Параметры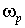 
и 
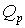определяют полюсы передаточной функции:
.
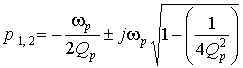При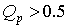 
полюсы 
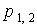комплексно-сопряженные. Параметр 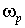называют частотой, а 
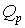– добротностью реализуемой пары полюсов.
Коэффициенты числителя передаточной функции определяют расположение нулей передачи и соответственно тип передаточной функции. Передаточную функцию фильтра нижних частот получим, предположив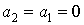 
:
.
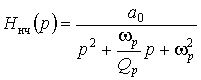Нули передачи фильтра верхних частот расположены в начале координат, поэтому
.
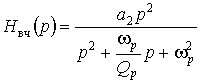Передаточная функция полосно-пропускающего фильтра
.
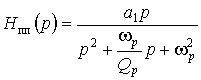В практике проектирования активных фильтров используется большое число схем, реализующих передаточные функции первого и второго порядков. Простейшими являются схемы на одном ОУ с положительной обратной связью. На рис. 8.7 показан фильтр нижних частот Саллена – Ки. Он назван так по фамилиям инженеров П. Саллена и Э. Ки, предложивших первые практические схемы активных фильтров. Операционный усилитель, резисторы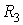 
и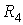 
реализуют неинвертирующий усилитель с коэффициентом усиления 
.
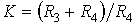Передаточная функция фильтра
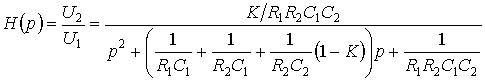.Для реализации фильтра верхних частот необходимо поменять местами резисторы 
, 
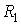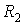и конденсаторы 
, 
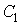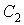. Достоинства фильтра Салле-на – Ки – простота структуры, минимальное число активных элементов. Последнее особенно важно в тех случаях, когда необходимо уменьшить мощность, потребляемую фильтром.
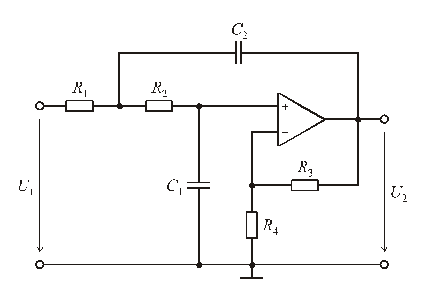
Рис. 8.7
В настоящее время разработаны различные процедуры расчета элементов фильтров Салена – Ки. Приведем один из вариантов, обеспечивающий равенство номиналов элементов. Исходными данными являются частота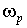 
и добротность полюсов 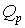. Расчет проводится в следующем порядке.
1. Выбираем подходящие номиналы конденсаторов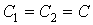 
.
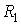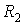2. Сопротивления резисторов и определяем по формуле
.
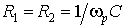Коэффициент передачи усилителя
.
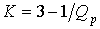Пример 8.2. Рассчитать фильтр нижних частот второго порядка, имеющий параметры: частота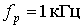 
, добротность полюсов 
.
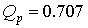Решение. Выбираем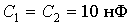 
. Сопротивления резисторов 
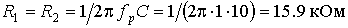. Коэффициент усилителя 
.
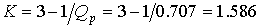Для реализации передаточных функций полосно-пропускающих фильтров с невысокой добротностью полюсов (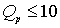
) используют звенья с многопетлевой обратной связью (рис. 8.8).
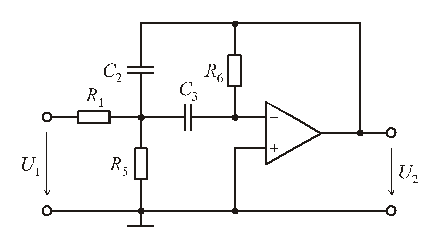
Рис. 8.8
Передаточная функция фильтра, показанного на рис. 8.8,
.
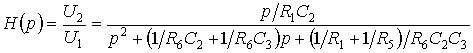Расчет элементов схемы проводится в следующем порядке.
1.Выбираем подходящие значения емкостей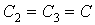 
.
2.Сопротивления резисторов рассчитываем по формулам:
; 
; 
.
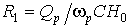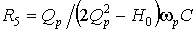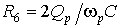В последних соотношениях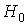 
– коэффициент передачи на частоте 
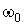. Для упрощения схемы можно исключить резистор 
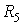, заменив его разрывом. Однако при этом нельзя будет контролировать коэффициент 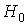. С помощью звеньев на одном ОУ можно реализовать и передаточные функции второго порядка с нулями передачи на мнимой оси. Однако такие звенья содержат большое число пассивных элементов. В частности, число конденсаторов может достигать трех-четырех. Значительно сложнее и процедуры расчета таких звеньев.
Главным недостатком звеньев на одном ОУ является высокая чувствительность характеристик к изменениям коэффициента усиления активного элемента. Особенно сильно это проявляется при реализации высокодобротных полюсов. В таких случаях используют звенья на нескольких ОУ. Их основные преимущества перед звеньями на одном ОУ заключаются в меньшей чувствительности характеристик, простоте регулировки и настройки. К тому же с точки зрения технологии интегральных схем минимизировать число активных элементов нецелесообразно. Поэтому звенья на нескольких ОУ часто оказываются более предпочтительными.
Универсальное звено на трех ОУ, реализующее одновременно передаточные функции ФНЧ, ФВЧ и ПФ, показано на рис. 8.9. Схема звена содержит два интегратора и сумматор. В зависимости от того, какой узел используется в качестве выходного, можно реализовать одну из трех передаточных функций:
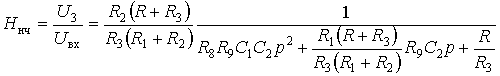; (8.6а)
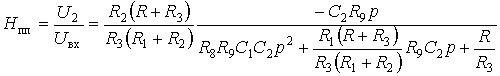; (8.6б)
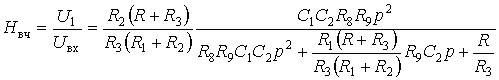. (8.6в)
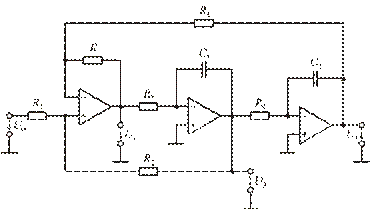
Рис. 8.9
Звенья на трех ОУ используют в универсальных модулях, изготавливаемых в виде интегральных схем. Такой модуль включает ОУ, конденсаторы и резисторы. Микросхема содержит внешние выводы для подключения источника питания, источника входного сигнала, а также регулировочных резисторов. С помощью таких резисторов можно регулировать характеристики фильтра (частоту 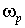и добротность полюсов 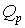). Модуль позволяет реализовать любую из передаточных функций (7.6).
