Определение 4: центроаффинным преобразованием с центром S называется аффинное преобразование пространства 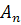 , оставляющее неподвижной точку S.
, оставляющее неподвижной точку S.
Пусть 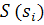 , применим к этой точке формулы (1) из §8, учитывая, что
, применим к этой точке формулы (1) из §8, учитывая, что 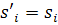 :
:
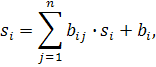
Откуда выразим 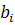 :
:
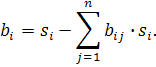
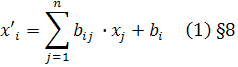
Подставив найденные значения снова в равенства (1) §8, получим формулы центроаффинного преобразования с центром S:
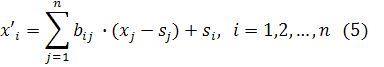
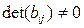 .
.
В частности, ели 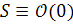 , то
, то 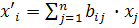 .
.
Композиция аффинных преобразований, оставляющих неподвижной точку S, есть аффинное преобразование, оставляющих неподвижной эту точку. Преобразование, обратное аффинному преобразованию, оставляющему точку S неподвижной, есть аффинное преобразование, также обладающие этими свойствами. Следовательно, центроаффинное преобразование с центром S образует группу, служащую еще одним примером подгруппы группы аффинных преобразований пространства 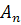 .
.
Теорема 2: всякое аффинное преобразование пространства 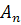 может быть представлено как композиция центроаффинного преобразования и параллельного переноса.
может быть представлено как композиция центроаффинного преобразования и параллельного переноса.
□ Из формул (1) §8 следует, что любое аффинное преобразование есть композиция центроаффинного преобразования
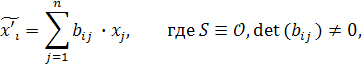
и параллельного переноса 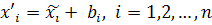 . ■
. ■
 2014-02-24
2014-02-24 1175
1175








