Для характеристики развития явления во времени применяются следующие показатели:
а) абсолютный прирост (Δ);
б) темп роста (Tp);
в) темп прироста (Tпр).
Рассматривая данные показатели, необходимо правильно выбирать базу сравнения, которая зависит от цели исследования. При сравнении каждого уровня ряда с предыдущим получаются цепные показатели; при сравнении каждого уровня с одним и тем же уровнем (базой) получают базисные показатели.
Для выражения абсолютной скорости роста (снижения) уровня ряда динамики исчисляют статистический показатель – абсолютный прирост (Δ). Его величина определяется как разность двух сравниваемых уровней. Она вычисляется по следующим формулам:
• цепной абсолютный прирост:
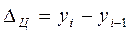 ;
;
• базисный абсолютный прирост:
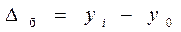 ,
,
где 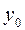 - уровень ряда динамики, выбранный за базу для определения базисных абсолютных приростов;
- уровень ряда динамики, выбранный за базу для определения базисных абсолютных приростов; 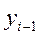 - уровень ряда динамики i -го года.
- уровень ряда динамики i -го года.
Интенсивность изменения уровней ряда динамики оценивается отношением текущего уровня к предыдущему или базисному, которое всегда представляет положительное число. Этот показатель принято называть темпом роста (Tp). Он выражается в процентах:
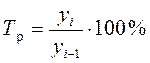 или
или 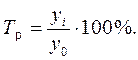
Темпы роста могут быть представлены в виде коэффициентов (Kp). В этом случае он показывает, во сколько раз данный уровень ряда больше уровня базисного года или какую его часть он составляет.
Для выражения изменения величины абсолютного прироста уровней ряда динамики в относительных величинах определяется темп прироста (Tпр), который рассчитывается как отношение абсолютного прироста к предыдущему или базисному уровню, т.е.
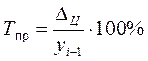 или
или 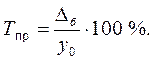
Существует связь между темпами роста и прироста:
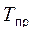 =
= 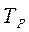 -100 %.
-100 %.
Между цепными и базисными показателями изменения уровней ряда существует следующая взаимосвязь:
а) сумма цепных абсолютных приростов равна базисному приросту:
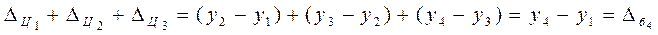 ;
;
б) произведение цепных коэффициентов роста равно базисному:
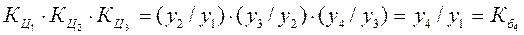 ;
;
в) деление рядом стоящих базисных коэффициентов роста друг на друга равно цепным коэффициентам роста:
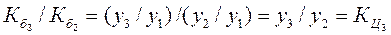 .
.
Взаимосвязь цепных и базисных темпов (коэффициентов) роста позволяет при анализе, если необходимо, переходить от цепных показателей к базисным и наоборот.
Для обобщения данных по рядам динамики рассчитываются:
• средний уровень ряда;
• средний абсолютный прирост;
• средний темп роста и прироста.
Для разных видов рядов динамики средний уровень рассчитывается неодинаково.
По интервальному динамическому ряду с равными интервалами средний уровень определяется по средней арифметической простой из уровней ряда:
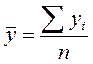 ,
,
где 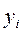 - уровни ряда для i -го периода; n – число уровней в ряду динамики.
- уровни ряда для i -го периода; n – число уровней в ряду динамики.
По моментному динамическому ряду с равными интервалами средний уровень определяется по формуле средней хронологической:
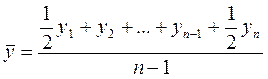 .
.
Данная формула используется, например, для расчета среднегодовой стоимости имущества при уплате налога на имущество.
Рассмотрим пример. На балансе предприятия числится имущество: на 01.01 – 800 тыс. руб., на 01.04 – 1000; на 01.07 – 1600; на 01.10 – 1100, на 01.01 следующего года – 1400 тыс. руб. Определим среднюю стоимость имущества для каждого квартала. Если мы знаем стоимость имущества на начало и на конец квартала, то средней оценкой стоимости на протяжении всего квартала будет простая арифметическая средняя из крайних значений:
I квартал ‑ 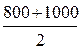 ; II квартал ‑
; II квартал ‑ 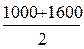 ; III квартал ‑
; III квартал ‑ 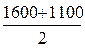 ;
;
IV квартал ‑ 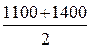 .
.
Можно сказать, что таким образом мы перешли от моментных показателей к интервальным. Теперь рассчитать среднюю стоимость имущества за год не составит труда. Для этого можно сложить квартальные средние и поделить их сумму на 4:
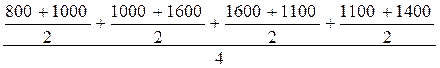 .
.
Нетрудно видеть, что данная формула преобразуется в среднюю хронологическую, а именно:
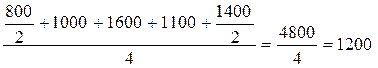 тыс. руб.
тыс. руб.
Кроме среднего уровня, при анализе и прогнозировании широко используются средние показатели изменения уровней ряда, а именно средний абсолютный прирост и средний темп роста.
Средний абсолютный прирост определяется как средняя арифметическая простая из цепных приростов:
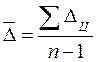 .
.
Так как 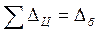 , то средний абсолютный прирост можно определять следующим образом:
, то средний абсолютный прирост можно определять следующим образом:
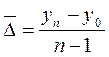 ,
,
где n ‑ число уровней ряда динамики; 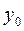 ‑ уровень ряда динамики, взятый за базу сравнения;
‑ уровень ряда динамики, взятый за базу сравнения; 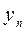 ‑ последний уровень ряда динамики;
‑ последний уровень ряда динамики;
Для обобщения характеристики интенсивности роста рассчитывается средний коэффициент (темп) роста по средней геометрической простой:
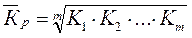 ,
,
где 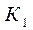 ,
, 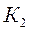 ,…,
,…, 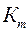 ‑ цепные коэффициенты роста; m – число цепных коэффициентов роста.
‑ цепные коэффициенты роста; m – число цепных коэффициентов роста.
Учитывая взаимосвязь цепных и базисных коэффициентов роста, средний коэффициент (темп) роста можно представить следующим образом:
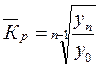 ,
,
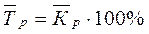 .
.
Средний темп прироста:
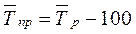 .
.
 2015-05-20
2015-05-20 487
487







