2015-05-20
474
При рассмотрении движения жидкостей наблюдается целый ряд новых переменных, которых не было при рассмотрении жидкости в равновесии.
Основной переменной является время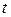 
, и в зависимости от нее могут изменяться все остальные величины, характеризующие движение.
В общем случае на жидкость действуют силы массовые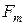 
и поверхностные 
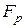.Изучение законов движения жидкости начинается с гидромеханики невязкой (идеальной) жидкости, т.е. без учета сил трения, а затем в зависимости вводят уточнения, полученные на основе экспериментальных данных.
Обозначая проекции на оси координат ускорений объемных сил через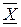 
, 
, 
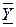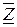, проекции на оси координат скорости точки через 
, 
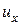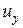и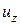 
, гидродинамическое давление в точке - 
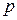и плотность - 
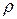, получаем восемь величин, характеризующих движение каждой частицы жидкого тела.
Задача гидродинамики — установить зависимости этих величин от координат времени 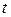и пространства 
, 
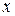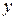и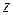 
.
Выведем основные дифференциальные уравнения, устанавливающие эту зависимость. Выделим в движущейся жидкости элементарно малый объем в форме параллелепипеда.
Воспользуемся полученными ранее (Тема: “Дифференциальные уравнения равновесия жидкости”) уравнениями равновесия. К действующим на элементарный параллелепипед силам присоединим также силы инерции.
Сумма проекций всех сил на ось 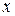(включая силу инерции 
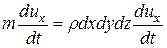), после сокращения на 
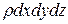дает нам уравнение:
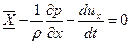. (3.9)
Составляя аналогичные уравнения относительно осе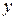й и 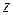, получаем систему уравнений:
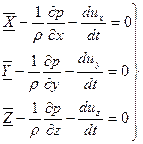. (3.10)
Так как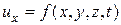 
- функция четырех переменных, то ее полный дифференциал равен:
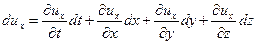. (3.11)
Разделив все члены этого полного дифференциала на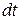 
, получим:
,
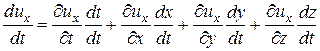аналогично можно представить
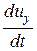и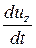 
.
Производные от координаты движущейся точки по времени представляют собой соответствующие проекции ее скорости. Подставляя производные в уравнение и перенеся члены, содержащие скорость, в правую часть, получим систему общих дифференциальных уравнений движения жидкого тела (Эйлер, 1755г.):
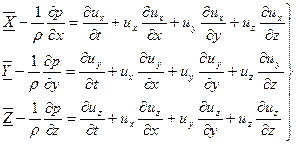. (3.12)
