Средняя является обобщающим показателем, с помощью которого можно охарактеризовать совокупность по количественно варьирующему признаку. Она отражает то общее, что складывается во всей совокупности и незаметно в отдельном объекте. Благодаря этому средняя получает большое значение для выявления закономерностей, присущих массовым явлениям.
Для осреднения различных признаков используются разные виды средних величин. Выбор вида средней осуществляется индивидуально в каждом случае и зависит от наличия исходных данных и вида признака.
Каждый вид средней имеет две формы: простую и взвешенную. Простая средняя используется в тех случаях, когда каждое значение признака встречается только один раз. Если некоторые значения признака повторяются неоднократно, т.е. данные сгруппированы, для расчета средней используются взвешенные формы.
Основные обозначения:
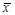 - среднее значение признака;
- среднее значение признака;
хi - индивидуальные значения осредняемого признака;
n - количество единиц совокупности;
fi - частота (вес) индивидуальных значений осредняемого признака;
wi = xi fi - произведение индивидуального значения признака и его частоты.
Таблица 2 - Виды и формы средних величин
| Виды средних величин | Простая | Взвешенная |
| 1 | 2 | 4 |
| 1. Арифметическая | 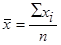 (8) (8)
| 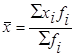 (9) (9)
|
| 2. Гармоническая | 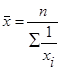 (10) (10)
| 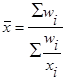 (11) (11)
|
| 3. Квадратическая | 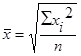 (12) (12)
| 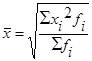 (13) (13)
|
| 4. Геометрическая | 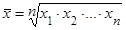 (14) (14)
| 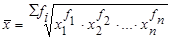 (15) (15)
|
| 5. Хронологическая | 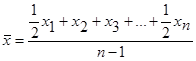 (16) (16)
|
Чаще всего используются простая и взвешенная арифметическая средняя.
В том случае, когда нет данных о частотах отдельных признаков, но имеются сведения о произведении индивидуального значения признака на его частоту, среднюю арифметическую можно заменить средней гармонической. При этом гармоническая простая используется только тогда, когда равны объемы совокупностей.
Средняя квадратическая, простая и взвешенная, используется, как правило, для расчета средних отклонений.
Геометрическая средняя используется для осреднения таких признаков, для которых характерна мультипликативная зависимость. Чаще всего гармоническая средняя используется для расчета средних темпов роста и средних индексов.
Хронологическая средняя применяется для расчетов средних уровней в моментных рядах динамики.
При расчете среднего значения признака в интервальных вариационных рядах используется средняя арифметическая взвешенная, определяемая по формуле (9) (табл.2). В этом случае за 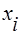 принимается середина каждого интервала, определяемая как полусумма максимального и минимального значения признака в группе.
принимается середина каждого интервала, определяемая как полусумма максимального и минимального значения признака в группе.
Например, если группировочный интервал 8-10, за 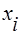 будет принято число 9, так как полусумма максимального и минимального значения признака в группе будет определена следующим образом:
будет принято число 9, так как полусумма максимального и минимального значения признака в группе будет определена следующим образом:
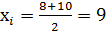
При наличии открытых интервалов, у которых определена только одна граница – верхняя или нижняя, открытый интервал принимается равным по величине смежному с ним закрытому интервалу. Например, если имеется интервальный ряд распределения:
| Объем продаж, тыс. руб. | Количество предприятий, шт. |
| до 100 | |
| 100-140 | |
| 140-180 | |
| свыше 180 |
У первой группы имеется открытый интервал, у которого указана только верхняя граница. В нашем случае, он принимается равным по величине второму интервалу, т. е. считается, что у первой группы объем продаж составит от 60 до 100 тыс. руб. Серединой интервала в данном случае будет объем продаж, равный 80 тыс. руб. (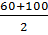 ).
).
Открытый интервал у последней группы принимается равным по величине предшествующему интервалу, т. е. примет значения от 180 до 220 тыс. руб., а середина интервала будет рассчитана (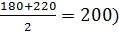 )
)
Средний объем продаж по данной совокупности определим так:
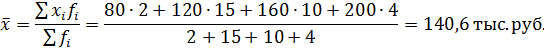
 2015-05-20
2015-05-20 347
347








